Kirchhoff's's Law of Current
Kirchhoff's law of current states that the algebraic sum of all current at any node (or junction) in an electrical circuit is equal to zero or equivalently the sum of the currents flowing into a node is equal to the sum of the currents flowing out of that node.
\[ \sum i_{in} = \sum i_{out} \]
At the node \( N \) above, we may write
\( i_1 + i_2 = i_3 + i_4 \)
Use Kirchhoff's Law of Current to Solve Current Problems
Example 1
Find current \( i_3 \) at the node shown below.
Solution to Example 1
Currents \( i_1 \) and \( i_2 \) are flowing into the node and currents \( i_3 \) and \( i_4 \) are flowing out of the node. Apply Kirchhoff's law of current at the given node.
\( i_1 + i_2 \) = \( i_3 + i_4 \)
Substitute the known quantities
\( 2 + 9 = i_3 + 4 \)
Solve for \( i_3 \)
\( i_3 = 7\) A
Example 2
Find currents \( i_3 \) and \( i_4 \) at the nodes \( N_1 \) and \( N_2 \) shown below.
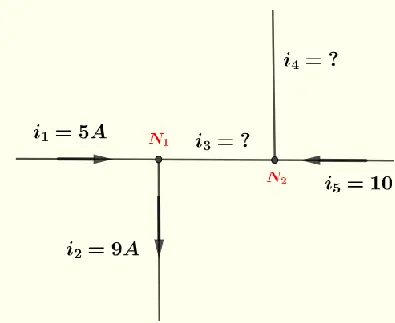
Solution to Example 2
We are not given any information on whether \( i_3 \) and \( i_4 \) flow into or out of the nodes. We assume \( i_3 \) flowing out of node \( N_1 \) and \( i_4 \) flowing out of node \( N_2 \) as shown below (in red) and use Kirchhoff's current law.
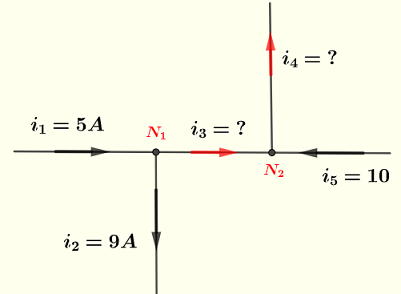
At node \( N_1 \), \( i_1 \) flows into \( N_1 \) and \( i_2 \) and \( i_3 \) flow out of \( N_1 \), and hence
\( i_1 \) = \( i_2 \) + \( i_3 \)
Substitute by known quantities
\( 5 \) = \( 9 \) + \( i_3 \)
Solve for \( i_3 \)
\( i_3 = - 4\)
Because \( i_3 \) is negative, \( i_3 \) flows into node \( N_1 \)
At node \( N_2 \), \( i_3 \) and \( i_5 \) flows into \( N_2 \) and \( i_4 \) flows out of \( N_2 \), and hence
\( i_3 + i_5 \) = \( i_4 \)
Substitute by known quantities
\( - 4 + 10 \) = \( i_4 \)
Solve for \( i_4 \)
\( i_4 = 6 \)
Because \( i_4 \) is positive it therefore flows out of node \( N_2 \)
Kirchhoff's Law of Voltage
Kirchhoff's law of voltage states that in any closed loop in an electrical circuit, the algebraic sum of all voltages around the loop is equal to zero.
\[ \sum v_{k} = 0 \]
Using the closed loop, we may write
\( e - V_{R_1} - V_{R_2} = 0 \)
Note: The voltage polarities for voltage sources and voltages across passive components such as resistor has to be respected and the signs taken care of.
Use Kirchhoff's Law of Voltage to Solve Voltage Problems
Example 3
Use Kirchhoff's Law of Voltage and all possible closed loops to write equations involving voltages in the circuit below and explain the signs of the voltages.
Solution to Example 3
Step 1: Set negative and positive polarities for all voltages (sources and across passive components). See diagram above
Step 2: Set arrows from the negative to the positive polarity of each voltage. See diagram above.
Step 3: Use Kirchhoff's Law of Voltage to write the equation following the rule:
As we go around the loop, if the arrow of the voltage is in the same direction as the loop it is "counted" as a positive voltage and if it is against it is "counted" as a negative voltage.
Loop \( L_1 \): The arrow of the voltage source \( e \) is in the same direction as the loop and hence positive. The arrows of voltages \( V_{R_1} \) and \( V_{R_2} \), across the resistors, are against the direction of the loop and hence negative.
Kirchhoff's Law for loop \( L_1 \) gives:
\( e - V_{R_1} - V_{R_2} = 0 \)
Loop \( L_2 \): The arrows of the voltage \( V_{R_2} \) is in the same direction of the loop and hence positive. The arrows of voltages \( V_{R_2} \), is against the direction of the loop and hence negative.
Kirchhoff's Law for loop \( L_2 \) gives:
\( V_{R_2} - V_{R_3 } = 0 \)
Loop \( L_3\): The arrows of the voltage source \( e \) is in the same direction as the loop and hence positive. The arrows of voltages \( V_{R_1} \) and \( V_{R_3} \), are against the direction of the loop and hence negative.
Kirchhoff's Law for loop \( L_3 \) gives:
\( e - V_{R_1} - V_{R_3 } = 0 \)
Example 4
In the circuit below \( e_1 = 20 \) Volts, \( V_{R_2} = 5 \) Volts and \( e_2 = 10 \) Volts. Find the voltages \( V_{R_2} \) and \( V_{R_3} \).
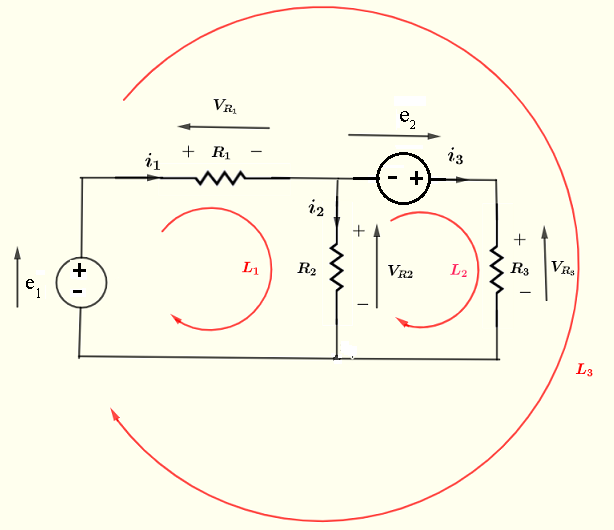
Solution to Example 4
Apply Kirchhoff's law of voltage to loop \(L_1 \) and write the equation
\( e_1 - V_{r_1} - V_{R_2} = 0 \)
Substitute the known quantities
\( 20 - 5 - V_{R_2} = 0 \)
Solve for \( V_{R_2} \)
\( V_{R_2} = 15 \) A
Apply Kirchhoff's law of voltage to loop \(L_2 \) and write the equation
\( V_{r_2} + e_2 - V_{R_3} = 0 \)
Substitute the known quantities
\( 15 + 10 - V_{R_3} = 0 \)
Solve for \( V_{R_3} \)
\( V_{R_3} = 25 \)
Important Note
What about loop \( L_3 \)?
Apply Kirchhoff's law of voltage to loop \(L_3 \) and write the equation
\( e_1 - V_{R_1} + e_2 - V_{R_3} = 0 \)
Substitute the known quantities
\( 20 - 5 + 10 - 25 = 0\)
The above equation is already satisfied. The mathematical meaning is that some of the equations given by Kirchhoff's law of voltage are not independent.