Kirchhoff's and Ohm's laws are used to solve DC circuits problems.
There are 3 examples; solve in the order that they are presented; this will make it easier to fully understand them.

Problem 1
Find current \( i \), voltages \( V_{R_1} \) and \( V_{R_2} \) in the ciruit below given that the voltage source \( e = 20 \) Volts, the resistances \( R_1 = 100 \; \Omega \) and \( R_2 = 300 \; \Omega \).

Solution to Problem 1
Apply Kirchhoff's law of voltage to the closed loop in the circle and write the equation
\( e - V_{R_1} - V_{R_2} = 0 \)     (1)
Use Ohm's law to write
\( V_{R_1} = i R_1 \) and \( V_{R_2} = i R_2 \)
Substitute \( V_{R_1} \) and \( V_{R_2} \) by their expression in equation (1)
\( e - i R_1 - i R_2 = 0 \)
Rearrange the above so that all term containing \( i \) are on one side
\( i R_1 + i R_2 = e \)
Factor \( i \) out
\( i ( R_1 + R_2) = e \)
Solve for \( i \)
\( i = \dfrac{e}{R_1 + R_2} \)
Substitute known quantities
\( i = \dfrac{20}{100 + 300} = 0.05 \) A
Calculate \( V_{R_1} \) and \( V_{R_2} \) using Ohm's law
\( V_{R_1} = i R_1 = 0.05 \times 100 = 5 \) V
\( V_{R_2} = i R_2 = 0.05 \times 300 = 15\) V

Problem 2
Given the voltage sources \( e_1 = 20 \) V, \( e_2 = 5 \) V, and the resistances \( R_1 = 100 \; \Omega \) , \( R_2 = 300 \; \Omega \) and \( R_3 = 50 \; \Omega \), find all currents through and voltages across the resistors in the circuit.

Solution to Problem 2
Kirchhoff's Law of voltage for all three loops \( L_1 \) , \( L_2 \) and \( L_3 \) gives
Loop \( L_1 \): \( e_1 - V_{R_1} - V_{R_2} = 0 \)      (1)
Loop \( L_2 \): \( V_{R_2} + e_2 - V_{R_3 } = 0 \)      (2)
Loop \( L_3 \): \( e_1 - V_{R_1} + e_2 - V_{R_3 } = 0 \)      (3)

Note that if we add equations (1) and (2), we obtain equation (3). Hence any 2 equations from the 3 can be used to solve the given problems. The third one does not give any extra information.
We have 3 unknowns, we therefore need another equation independent from the above equation.
Kirchhoff's Law of current applied at node A gives
\( i_1 = i_2 + i_3 \)      (4)

So we select equations (1), (2) and (4) to write the system of equations
\( e_1 - V_{R_1} - V_{R_2} = 0 \)      (5)
\( V_{R_2} + e_2 - V_{R_3 } = 0 \)      (6)
\( i_1 = i_2 + i_3 \)      (7)

Use Ohm's law to rewrite \( V_{R_1} \) and \( V_{R_2} \) as follows
\( V_{R_1} = R_1 i_1 \) and \( V_{R_2} = R_2 i_2\)
Substitute the above in equations (5) and (6) and rewrite the system of equations (5), (6) and (7) as
\( R_1 i_1 + R_2 i_2 = e_1 \)      (8)
\( R_2 i_2 - R_3 i_3 = - e_2 \)      (9)
\( i_1 = i_2 + i_3 \)      (10)

Substitute the known quantities by their numerical values to obtain a linear system system of equations with three unknowns \( i_1 \), \( i_2\) and \( i_3 \) .
\( 100 i_1 + 300 i_2 = 20 \)      (11)
\( 300 i_2 - 50 i_3 = - 5 \)      (12)
\( i_1 = i_2 + i_3 \)      (13)
There are many ways to solve the above system.
One way is to use equation (XIII) and substitute \( i_1 \) by \( i_2 + i_3 \) in equations (XI) and (XII) to obtain a system with two unknowns
\( 100 (i_2 + i_3) + 300 i_2 = 20 \)      (14)
\( 300 i_2 - 50 i_3 = - 5 \)      (15)
Rearrange to rewrite the above system as
\( 400 i_2 + 100 i_3 = 20 \)      (16)
\( 300 i_2 - 50 i_3 = - 5 \)      (17)
Multiply all terms of equation (17) above by 2 and rewrite the above system as
\( 400 i_2 + 100 i_3 = 20 \)      (16)
\( 600 i_2 - 100 i_3 = - 10 \)      (17)
Add side by side equations (16) and (17) to obtain one equation in one variable
\( 1000 i_2 = 10 \)
Solve for \( i_2 \)
\( i_2 = 10/1000 = 0.01 \) A
Substitute \( i_2 \) by \( 0.01 \) in equation (16) and solve for \( i_3 \)
\( 400 \times 0.01 + 100 i_3 = 20 \)
Solve for \( i_3 \)
\( i_3 = 0.16 \) A
Use equation (13) to solve for \(i_1\)
\( i_1 = i_2 + i_3 = 0.01 + 0.16 = 0.17\) A
We now calculate the voltages across the resistors
\( V_{R_1} = R_1 I_1 = 100 \times 0.17 = 17 \) V
\( V_{R_2 } = R_2 I_2 = 300 \times 0.01 = 3 \) V
\( V_{R_3 } = R_3 I_3 = 50 \times 0.16 = 8\) V

Problem 3
Find all currents through and voltages across the resistors in the circuit below, given the voltage sources \( e_1 = 20 \) V, \( e_2 = 5 \) V, and the resistances \( R_1 = 100 \; \Omega \) , \( R_2 = 120 \; \Omega \), \( R_3 = 60 \; \Omega \), \( R_4 = 40 \; \Omega \), \( R_5 = 240\; \Omega \) and \( R_6 = 80 \; \Omega \).


Solution to Problem 3
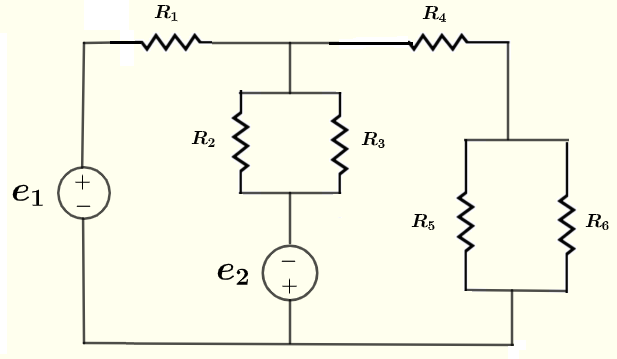
All the details of the solution are presented and in order to make this presentation clear and easy to understand, the solution of this example has 5 parts.

Part 1: Simplify the circuit by grouping resistors
If we apply Kirchhoff's law to the closed loops and nodes in the given circuit above, we will end up with a large number of equations to solve.
However, a quick analysis of the given circuit shows that some of the resistors are parallel and series configurations as shown below.
Resistors \( R_2 \) and \( R_3 \) are in parallel and their equivalent resistance is \( R'_2 \) as shown in the circuit below.
\( R_5\) and \( R_6 \) are in parallel and their equivalent resistance is in series with \( R_4 \) and their overall equivalent resistance is \( R'_3 \) as shown in the circuit below.

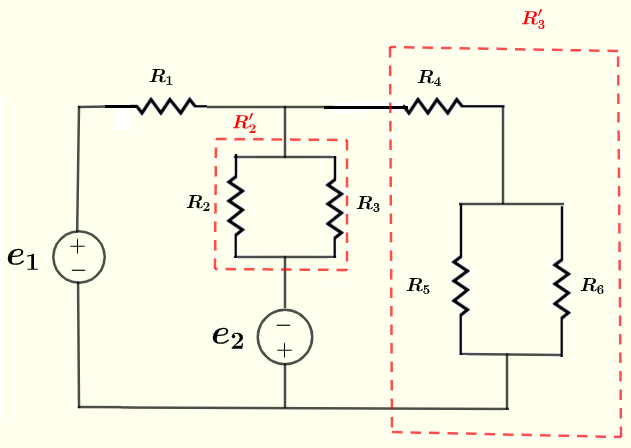
Use the formula for resistors in parallel to write
\( \dfrac{1}{R'_2} = \dfrac{1}{R_2} + \dfrac{1}{R_3} \)
Solve the above for \( R'_2 \) to obtain
\( R'_2 = \dfrac{R_2 \cdot R_3}{R_2 + R_3} \)
Substitute the knwon quantities to obtain
\( R'_2 = \dfrac{120 \cdot 60}{120 + 60} = 40 \; \Omega \)
Use formula for resistors in parallel to \( R_5\) and \( R_6 \) and add it to \( R_4 \) to write \( R'_3 \) as
\( R'_3 = R_4 + \dfrac{R_5 \cdot R_6}{R_5 + R_6} \)
Substitute the knwon quantities to obtain
\( R'_3 = 40 + \dfrac{240 \cdot 80}{240 + 80} = 100\)

Part 2: Calculate \( i_1 \), \( i_2 \) and \( i_3 \) using Kirchhoff's law
We now have a much simpler circuit to solve as shown below.


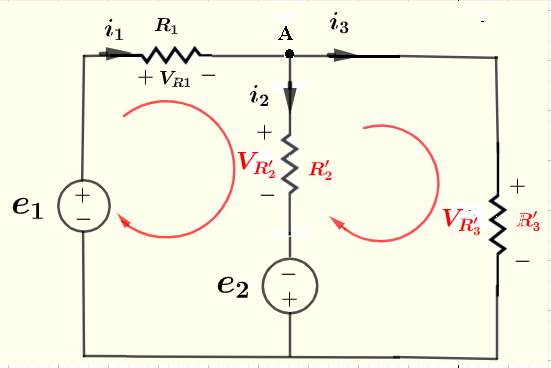
There are 3 unkwons \( i_1 \), \( i_2 \) and \( i_3 \) and we therefore need 3 equations.
Use Kirchhoff's law of current at node A to write
\( i_1 = i_2 + i_3 \)      (1)
Use Use Kirchhoff's law of voltage for the loop on the left
\( e_1 - V_{R_1} - V_{R'_2} + e_2 = 0 \)      (2)
Use Use Kirchhoff's law of voltage for the loop on the right
\( - e_2 + V_{R'_2} - V_{R'_3} = 0 \)      (3)
Use Ohm's law to write
\( V_{R_1} = R_1 i_1 \)
\( V_{R'_2} = R'_2 i_2 \)
\( V_{R'_3} = R'_3 i_3 \)
Substitute the above voltages in equations (2) and (3) and include equation (1) to rewrite the system of 3 equations with 3 unknowns
\( e_1 - R_1 i_1 - R'_2 i_2 + e_2 = 0 \)
\( - e_2 + R'_2 i_2 - R'_3 i_3 = 0 \)
\( i_1 = i_2 + i_3 \)
Substitute the knwon quantities, simplify and rewrite the above system in the form.
\( 100 i_1 + 40 i_2 = 25\)      (4)
\( 40 i_2 - 100 i_3 = 5 \)      (5)
\( i_1 = i_2 + i_3 \)      (6)
There are many ways to solve systems of linear equations. Let us use the method of substitution.
Substitute \( i_1 \) by \( i_2 + i_3 \) in equations (4) and rewrite equations (4) and (5) as follows
\( 100 (i_2 + i_3) + 40 i_2 = 25\)      (7)
\( 40 i_2 - 100 i_3 = 5 \)      (8)
Simplify and group
\( 140 i_2 + 100 i_3 = 25\)
\( 40 i_2 - 100 i_3 = 5 \)
Add the above equations to eliminate \( i_3 \)
\( 180 i_2 = 30 \)
Solve for \( i_2 \)
\( i_2 = 30/180 = 1/6 \) A
Use equation (7) (or (8) ) to find \( i_3 \)
\( 100 i_3 = 25 - 140 i_2 \)
\( i_3 = 1/60 \) A
Use equation (6) to find \( i_1 \)
\( i_1 = i_2 + i_3 = 1/6 + 1/60 = 11/60\)

Part 3: Calculate currents in resistors \( R_2 \) and \( R_3 \)

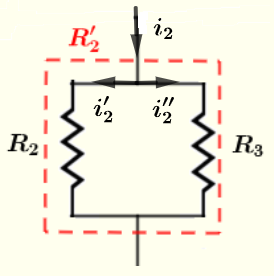
Apply Kirchhoff's law of current
\( i_2'+i_2'' = i_2 = 1/6 \)
Kirchhoff's law of voltage to the closed loop.
\( R_2 i_2' - R_3 i_2'' = 0 \)
Substitute known quantities in the above equation
\( 120 i_2' - 60 i_2'' = 0 \)
Solve the system of 2 equations 2 unknowns
\( i_2'+i_2'' = 1/6 \)
\( 120 i_2' - 60 i_2'' = 0 \)
to obtain
\( i_2' = 1/18 \) A
and \( i_2'' = 1/9 \) A

Part 4: Calculate currents in resistors \( R_5 \) and \( R_6 \)
We now calculate the currents through resistors \( R_5 \) and \( R_6 \) using the circuit below


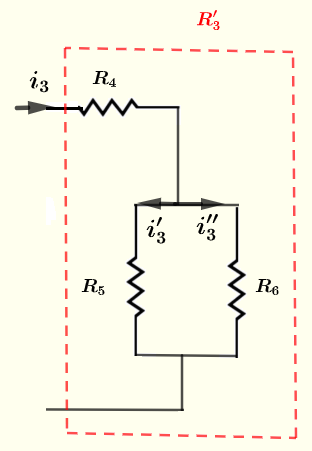
Apply Kirchhoff's law of current
\( i_3'+i_3'' = i_3 = 1/60 \)
Kirchhoff's law of voltage to the closed loop.
\( R_5 i_3' - R_6 i_3'' = 0 \)
Substitute known quantities in the above equation
\( 240 i_2' - 80 i_2'' = 0 \)
Solve the system of 2 equations 2 unknowns
\( i_3'+i_3'' = 1/60 \)
\( 240 i_2' - 80 i_2'' = 0 \)
to obtain
\( i_3' = 1/240 \)A
and \( i_3''' = 1/80 \) A

Part 5: Calculate voltages in all resistors
We now list all resistors and the currecnts through each one of them; and then calculate the voltages across each one of them.
\( R_1 = 100 \; \Omega \) , current \( i_1 = 11/60 \) A     voltage : \( V_{R_1} = 100 \times 11/60 = 18.33 \) V
\( R_2 = 120 \; \Omega \) , current \( i_2' = 1/18 \) A     voltage : \( V_{R_2} = 120 \times 1/18 = 6.67 \) V
\( R_3 = 60 \; \Omega \) , current \( i_2'' = 1/9 \)A     voltage : \( V_{R_3} = 60 \times 1/9 = 6.67 \) V
\( R_4 = 40 \; \Omega \) , current \( i_3 = 1/60 \) A     voltage : \( V_{R_4} = 40 \times 1/60 = 0.67 \) V
\( R_5 = 240\; \Omega \) , current \( i_3' = 1/240 \)A     voltage : \( V_{R_5} = 240 \times 1/240 = 1 \) V
\( R_6 = 80 \; \Omega \) , current \( i_2'' = 1/80 \)A     voltage : \( V_{R_5} = 80 \times 1/80 = 1 \) V

More References and Links