Components of a Force in a System of Coordinates
Components of a Force
Being a vector
, a force
can be represented by its components like any vector. One of the main advantage of resolving forces into their components, is that it is easy to add them, to scalar multiply them, etc.
If |F| is the magnitude and θ is the angle between the positive direction of the x-axis and the force F, then the components Fx and Fy are given by
Fx = |F| cosθ and Fy = |F| sinθ
Hence F may be written in terms of its components as follows
F = (Fx , Fy) = (|F| cosθ , |F| sinθ)
A video with more examples on Components of Vectors
and another video with more examples on Components of Forces are included.
Examples with Detailed Solutions
Example 1
Find the components of a force F whose magnitude is 20 N and its direction is defined by angle θ = 30° made by the force and the positive x-axis as shown below.
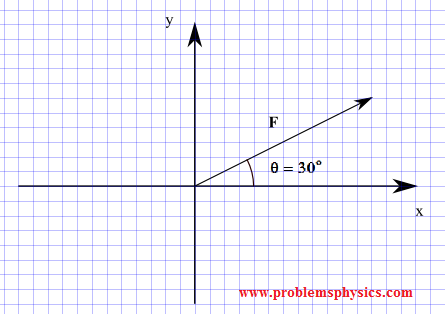
Solution
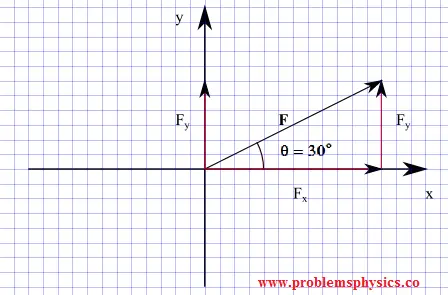
Let the components of force (vector) F be Fx and Fy as shown in the diagram below.
Using the the right triangle made by F, Fx and Fy we can write
sin θ = Fy / |F|
cos θ = Fx / |F|
where |F| is the magnitude of force F.
The above may be written as
Fx = |F| cos θ = 20 cos 30° = 10 √3
Fy = |F| sin θ = 20 sin 30° = 10
F = (10 √3 , 10)
Example 2
Find the components of a force whose magnitude is 50 N and its direction is given by angle α = 25° made with the negative y-axis as shown in the diagram below.
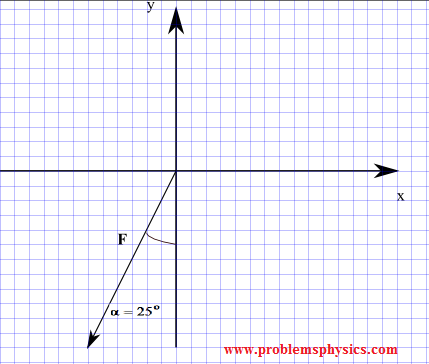 _
_
Solution

Let Fx and Fy be the components of F as shown in the diagram below.
Using the the right triangle made by F, Fx and Fy to write
sin α = - Fx / |F|
cos α = - Fy / |F|
The minus in - Fx / |F| and - Fy / |F| accounts for the fact that Fx and Fy are negative. Hence
Fx = - |F| sin α = - 50 sin 25° ≈ - 21.1
Fy = - |F| cos α = - 50 cos 25° ≈ - 45.3
F = (- 21.1 , - 45.3)
Example 3
In the diagram below, force F is parallel to the leg CB of the right triangle ABC.
a) Determine the components of the force F in terms of the magnitude of F and angle α. The rectangular system x-y has the x-axis parallel to AC and the y axis perpendicular to AC as shown in the diagram.
b) Find numerical values of the components for |F| = 100m N and α = 30°.
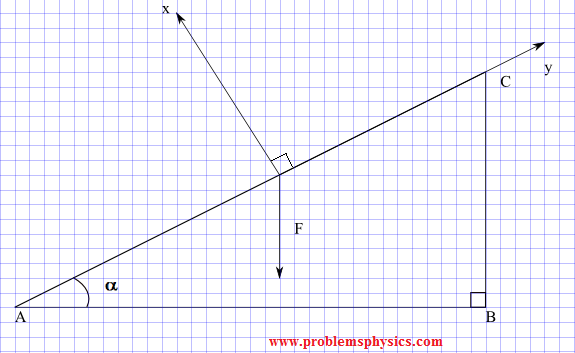
Solution
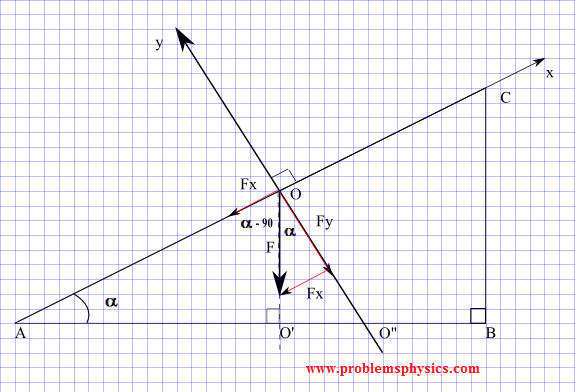
The right triangle AOO' has angle α, 90°-α and 90°.
Since AC is perpendicular to OO", angle AOO' is equal to 90° and therefore angle O'OO" is equal to α
Consider the right triangle made by F, Fy and Fx.
sin α = - Fx / |F| (the minus sign is due to the fact that Fx is negative)
cos α = - Fy / |F| (the minus sign is due to the fact that Fy is negative)
which gives
Fx = - |F| sin α
Fy = - |F| cos α
F = (- |F| sin α , - |F| cos α)
|F| = 100 , α = 30°
Fx = - |F| sin α = -100 sin 30° = - 50
Fy = - |F| cos α = -100 cos 30° = - 50 √ 3
F = (-50 , - 50 √ 3)
Note: The above example is very useful in problems related to forces in incline plane.
Example 4
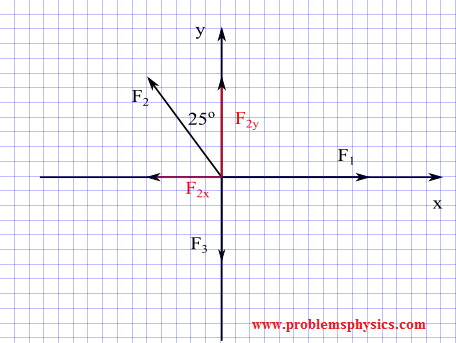
Three forces F1, F2 and F3 of magnitudes 80 N, 60 N and 50 N in the same system of axes such that F1 is directed along the positive x axis; F2 in the direction given by the bearing N25E and F3 along the negative y axis.
Find the components of each force.
Solution
We first construct a diagram using the directions given above.
F1 is directed along the x axis, hence one component along the x axis equal to |F| and the component along y -axis is equal to 0
F1 = (|F1| , 0) = (80 , 0)
F2 is directed along the negative y axis, hence
F2 = (0 , -|F2|) = (0 , - 60)
F3 is such that the x component is negative and the y component is positive; using the right triangle made by F2, F2x and F2y we write
F3 = (F2x , F2y) = (-60 sin 25° , 60 cos 25°)
Example 5
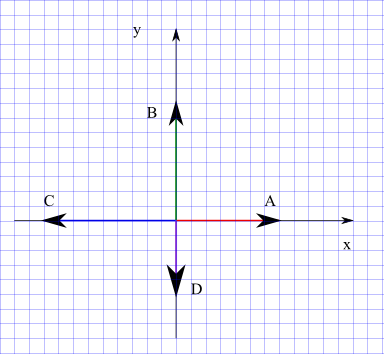
Express each of the forces A, B, C and D shown in the figure below by its components.
Solution
Each of the four forces is directed either along the x or the y axis in the negative or positive direction.
A = (|A| cos 0° , |A| sin 0°) = ( |A| , 0)
B = (|B| cos 90° , |B| sin 90°) = (0 , |B|)
C = (|C| cos 180° , |C| sin 180°) = (-|B| , 0)
D = (|D| cos 270° , |D| sin 270°) = (0 , -|C|)


 _
_




