Hooke's Law
In the diagram below is shown a block attached to a spring. In position (A) the spring is at rest and no external force acts on the block. In position (B) a force F is used to compress the spring by a length equal to Δ x by pushing the block to the left. In position (C), a force F is used to stretch the spring by a length Δ x by pulling the block to the right. Δ x is the change in the length of the spring measured from its position at rest.
In both cases, the relationship between the magnitude of force F used to stretch or compress the spring by a length Δ x is given by Hooke's law as follows:
where k is the spring constant.
According to Newton's third law, if a spring is stretched or compressed using force F, as a reaction the spring also react by a force - F.
Problems with Detailed Solutions
Problem 1
What is the magnitude of the force required to stretch a 20 cm-long spring, with a spring constant of 100 N/m, to a length of 21 cm?Solution
The spring changes from a length of 20 cm to 21 cm, hence it stretches by 1 cm or | Δ x | = 1 cm = 0.01 m.
| F | = k | Δ x | = 100 N / m × 0.01 m = 1 N
Problem 2
What is the spring constant of a spring that needs a force of 3 N to be compressed from 40 cm to 35 cm?Solution
The spring changes from a length of 40 cm to 35 cm, hence it stretches by 40 cm - 35 cm = 5 cm or | Δ x | = 5 cm = 0.05 m.
| F | = k | Δ x | = 3 N
k = | F | / | Δ x| = 3 / 0.05 = 60 N / m
Springs in Parallel
Two springs are said to be in parallel when used as in the figure below.
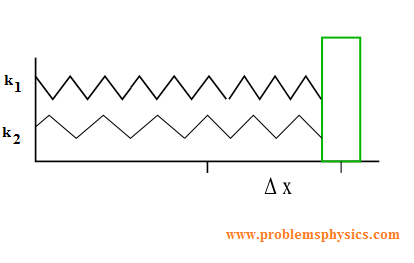
The two springs behave like on spring whose constant k is given by
Problem 3
What is the magnitude of the force required to stretch two springs of constants k1 = 100 N / m and k2 = 200 N / m by 6 cm if they are in parallel?Solution
The two springs behave like a spring with constant k given by
k = k1 + k2 = 100 N / m + 300 N / m
| F | = k | Δ x | = 300 N / m × 0.06 m = 18 N
Spring in Series
Two springs are said to be in series when used as in the figure below.
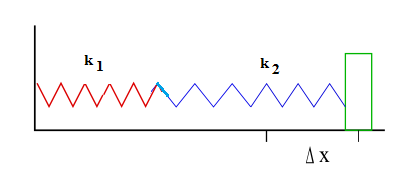
The two springs behave like on spring whose constant k is given by
Problem 4
What is the magnitude of the force required to stretch two springs of constants 100 N / m and 200 N / m by 6 cm if they are in series?Solution
The two springs behave like a spring with constant k obtained by solving for k the following
1 / k = 1 / 100 + 1 / 300
k = 75 N / m
| F | = k | Δ x | = 75 N / m × 0.06 m = 4.5 N
Potential Energy of a Spring
To stretch or compress a spring by a length | Δ x |, energy is needed. Once stretched or compressed, the energy is stored in the spring as potential energy P e and is given by:Problem 5
How much energy W is needed to compress a spring from 15 cm to 10 cm if the constant of the spring is 150 N / m?Solution
$ Δ x $ = 10 cm - 15 cm = - 5 cm = - 0.05 m
The energy W to compress the spring will all be stored as potential energy P e in the spring, hence
W = P e = (1/2) k (Δ x) 2 = 0.5 × 150 × (- 0.05) 2 = 0.1875 J
