Inclined plane problems are fundamental in physics, involving gravity, friction forces, and motion analysis. These problems require vector representations of physical quantities. Using rectangular coordinate system components simplifies force calculations and applications of Newton's laws.
Components are particularly useful for representing forces since they enable easier vector addition and equilibrium analysis. Free-body diagrams combined with Newton's second law ($\sum \vec{F} = m\vec{a}$) provide a systematic approach to solving these problems.
A helpful resource: Video tutorial on Vector Components.
A $2\text{ kg}$ box is placed on a frictionless inclined plane at $27^\circ$ to the horizontal.
a) Draw a free-body diagram showing all forces acting on the box.
b) Determine the acceleration of the box down the incline.
c) Find the normal force exerted by the incline on the box.
Solution
a) Free-body diagram:

Two forces act on the box: its weight $\vec{W}$ and the normal force $\vec{N}$ exerted by the incline.
b) Using coordinate axes aligned with the incline:

Vector components:
$\vec{N} = (0, N)$
$\vec{W} = (W_x, W_y) = (mg\sin27^\circ, -mg\cos27^\circ)$
$\vec{a} = (a, 0)$ (motion along the incline)
Applying Newton's second law ($\sum \vec{F} = m\vec{a}$):
$\vec{W} + \vec{N} = m\vec{a}$
Component equations:
$x$-component: $mg\sin27^\circ = ma$
$y$-component: $-mg\cos27^\circ + N = 0$
Solving for acceleration:
$a = g\sin27^\circ = (10\text{ m/s}^2)(0.454) \approx 4.54\text{ m/s}^2$
c) From the $y$-component equation:
$N = mg\cos27^\circ = (2\text{ kg})(10\text{ m/s}^2)(0.891) \approx 17.8\text{ N}$
A $5\text{ kg}$ particle rests on a $30^\circ$ incline. A force $F_a = 30\text{ N}$ acts parallel to the incline, directed upward.
a) Draw a complete free-body diagram.
b) Determine the friction force acting on the particle.
c) Find the normal force.
Solution
a) Free-body diagram:

Forces: weight $\vec{W}$, normal force $\vec{N}$, applied force $\vec{F}_a$, and static friction $\vec{F}_s$.
b) Force components with incline-aligned axes:

Since the particle is at rest ($\vec{a} = 0$):
$\vec{F}_a + \vec{W} + \vec{N} + \vec{F}_s = 0$
Component forms:
$\vec{F}_a = (30, 0)$
$\vec{W} = (-mg\sin30^\circ, -mg\cos30^\circ) = (-25, -25\sqrt{3})$
$\vec{N} = (0, N)$
$\vec{F}_s = (-F_s, 0)$
$x$-component equation:
$30 - 25 - F_s = 0$
$F_s = 5\text{ N}$
c) $y$-component equation:
$0 - 25\sqrt{3} + N + 0 = 0$
$N = 25\sqrt{3} \approx 43.3\text{ N}$
A $10\text{ kg}$ box rests on a $35^\circ$ incline. A string at $25^\circ$ to the incline holds the box. The coefficient of static friction is $\mu_s = 0.3$.

a) Draw a free-body diagram.
b) Find the tension $T$ in the string.
c) Determine the friction force magnitude.
Solution
a) Free-body diagram with forces: tension $\vec{T}$, weight $\vec{W}$, normal force $\vec{N}$, and friction $\vec{F}_s$.
b) Force components:
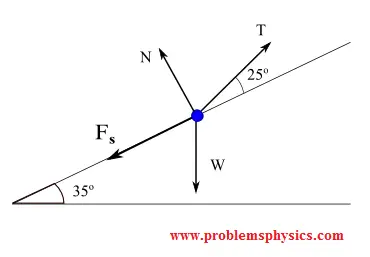

Equilibrium: $\vec{W} + \vec{T} + \vec{N} + \vec{F}_s = 0$
Component forms:
$\vec{W} = (-mg\sin35^\circ, -mg\cos35^\circ)$
$\vec{T} = (T\cos25^\circ, T\sin25^\circ)$
$\vec{N} = (0, N)$
$\vec{F}_s = (-\mu_s N, 0)$
$x$-component: $-mg\sin35^\circ + T\cos25^\circ - \mu_s N = 0$ (1)
$y$-component: $-mg\cos35^\circ + T\sin25^\circ + N = 0$ (2)
From (2): $N = mg\cos35^\circ - T\sin25^\circ$
Substitute into (1):
$-mg\sin35^\circ + T\cos25^\circ - \mu_s(mg\cos35^\circ - T\sin25^\circ) = 0$
Solve for $T$:
$T = \dfrac{\mu_s mg\cos35^\circ + mg\sin35^\circ}{\cos25^\circ + \mu_s\sin25^\circ}$
With $m=10\text{ kg}$, $g=10\text{ m/s}^2$, $\mu_s=0.3$:
$T = \dfrac{0.3 \times 100 \times 0.819 + 100 \times 0.574}{0.906 + 0.3 \times 0.423} \approx \dfrac{24.57 + 57.4}{0.906 + 0.127} \approx \dfrac{81.97}{1.033} \approx 79.4\text{ N}$
c) Friction force:
$F_s = \mu_s N = \mu_s(mg\cos35^\circ - T\sin25^\circ)$
$F_s = 0.3(100 \times 0.819 - 79.4 \times 0.423) \approx 0.3(81.9 - 33.6) \approx 14.5\text{ N}$
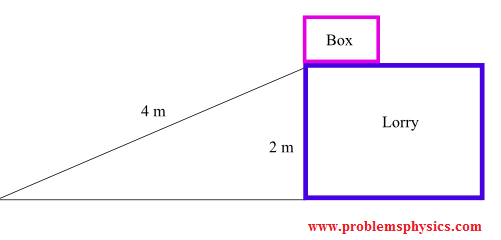
A $100\text{ kg}$ box is lowered at constant speed down a $4\text{ m}$ incline from a truck bed $2\text{ m}$ high. The kinetic friction coefficient is $\mu_k = 0.45$. Find the force $F_a$ applied parallel to the incline to maintain constant speed.
Solution
Free-body diagram with forces: applied force $\vec{F}_a$, weight $\vec{W}$, normal force $\vec{N}$, and kinetic friction $\vec{F}_k$.


Incline angle: $\sin\alpha = 2/4 = 0.5$, so $\alpha = 30^\circ$, $\cos\alpha = \sqrt{3}/2 \approx 0.866$
Constant speed $\Rightarrow$ acceleration $= 0$
Component equations:
$x$-component: $F_a + F_k - mg\sin\alpha = 0$ (1)
$y$-component: $N - mg\cos\alpha = 0$ (2)
From (2): $N = mg\cos\alpha$
Kinetic friction: $F_k = \mu_k N = \mu_k mg\cos\alpha$
Substitute into (1): $F_a = mg\sin\alpha - \mu_k mg\cos\alpha$
$F_a = 100 \times 10 (\sin30^\circ - 0.45\cos30^\circ)$
$F_a = 1000 (0.5 - 0.45 \times 0.866) \approx 1000(0.5 - 0.390) \approx 110\text{ N}$
A $7\text{ kg}$ box is on the verge of sliding down a $25^\circ$ incline. A horizontal force $F_a$ prevents sliding. The static friction coefficient is $\mu_s = 0.3$. Find $F_a$.

Solution
Free-body diagram with standard horizontal-vertical axes:

Force components:
$\vec{W} = (0, -mg)$
$\vec{N} = (-N\sin25^\circ, N\cos25^\circ)$
$\vec{F}_a = (F_a, 0)$
$\vec{F}_s = (\mu_s N\cos25^\circ, \mu_s N\sin25^\circ)$ (friction opposes impending motion down the incline)
Equilibrium equations:
$x$-component: $-N\sin25^\circ + F_a + \mu_s N\cos25^\circ = 0$ (1)
$y$-component: $-mg + N\cos25^\circ + \mu_s N\sin25^\circ = 0$ (2)
From (2): $N = \dfrac{mg}{\cos25^\circ + \mu_s\sin25^\circ}$
Substitute into (1):
$F_a = N\sin25^\circ - \mu_s N\cos25^\circ = N(\sin25^\circ - \mu_s\cos25^\circ)$
Combining expressions:
$F_a = mg \dfrac{\sin25^\circ - \mu_s\cos25^\circ}{\cos25^\circ + \mu_s\sin25^\circ}$
With $m=7\text{ kg}$, $g=10\text{ m/s}^2$, $\mu_s=0.3$:
$F_a = 70 \times \dfrac{0.423 - 0.3 \times 0.906}{0.906 + 0.3 \times 0.423} \approx 70 \times \dfrac{0.423 - 0.272}{0.906 + 0.127} \approx 70 \times \dfrac{0.151}{1.033} \approx 10.2\text{ N}$