What is the Tension of a String or rope?
What is the tension of a string?
The concept of tension of strings is used to explain the transmission of forces from one point to another. Consider the system of a box that hangs at rest from a ceiling as shown below.

1) According to the
free body diagram of the box, the forces acting on the box are: the weight of the box W and T '1 the force exerted by the string on the box.
Let x-y be a rectangular coordinate system and express W and T '1 by their components using magnitude and direction as follows:
W = (0 , -|W|) and T '1 = (0 , |T '1|)
Since the box is at rest, from Newton's second law, we have
W + T '1 = (0 , -|W|) + (0 , |T '1|) = 0
which gives
-|W| + |T '1| = 0 or |T '1| = |W|
T '1 and W have equal magnitude and opposite direction which explains why the box is at rest.
2) The forces acting on the string are the force T1 exerted by the box on the string as a reaction to T '1, T2 exerted by the ceiling on the string and w ' the weight of the string.
Using the same system of axes described above, we express T1, w ' and T2 in components form using magnitude and direction as follows
T1 = (0 , -|T1|)
T2 = (0 , |T2|)
w ' = (0 , -|w '|)
The string is also at rest, hence by Newton's second law, we have
T1 + T2 + w ' = (0 , -|T1|) + (0 , |T2|) + (0 , -|w '|) = 0
which gives
-|T1|+ |T2| - |w '| = 0
|T2| = |T1| + |w'|
If the weight of the string w ' is very small compared to |T2| and |T1|, it can be neglected and we end up with
|T2| = |T1|
Now since |T1| and |T2| are equal for massless strings, the effect of the string is to transmit forces between distant points through the tension in the string.
Note the tension has the same magnitude everywhere for a massless string (and frictionless pulley if used). The direction of the tension may or may not be the same.
T1 and T '1 are action-reaction pair and are therefore equal in magnitude and opposite side. T2 and T '2 are also action-reaction pair and are also equal in magnitude and opposite side. Hence we can finally write that
|T '1| = |T '2| which is mostly needed to solve problems involving strings, cords, ...
For a massless string or cord, the tension is the same everywhere.
Examples with Detailed Solutions
In all the examples below are the
free body diagram for several systems with strings and pulleys. Tension forces in the different strings are analysed. We assume that the strings used in the different systems have a very small mass and may be neglected. We also assume that the pulleys are frictionless and have have very small masses that may be neglected.
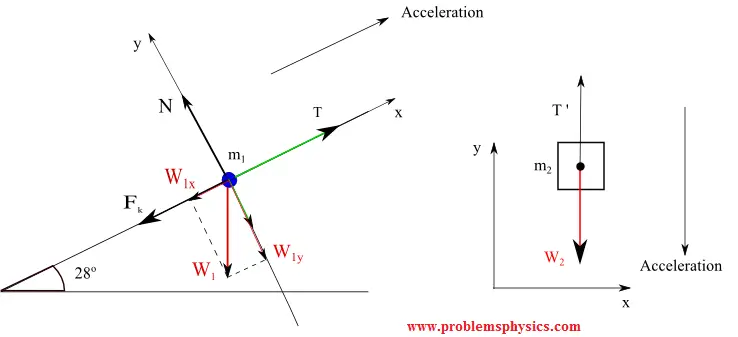
Example 1
In this example the tension of the string is the same and therefore the magnitude of T1, the force exerted by the string on block m1, and the magnitude of T2, the force exerted by the string on m2 are equal. Note that the directions of T1 and T2 are different.
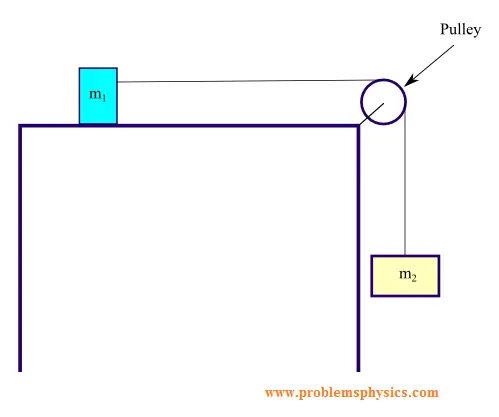

Example 2
In this example, the magnitudes of T1 and T2 are equal since they are related to the tension in the same string. T1 and T2 have the same direction.


Example 3
In this example, the magnitudes of T3 and T '3 are equal since they are related to the tension in the same string. The directions of of T3 and T '3 are opposite.


Example 4
In this example, the magnitudes of T1 and T '1 are equal (same string) but different directions. Also, the magnitudes of T2 and T '2 are equal (same string) but different directions.


Example 5
In this example, the magnitudes of T and T ' are equal (same string) and their directions are different.