Magnetic Forces on Electric Current-carrying conductors
Force Acting on a Current Carrying Wire
A current carrying wire of length L in a magnetic field B experiences a force F given

F is the force exerted on the wire, i is the current in the wire and B is the force all represented by vectors. Hence the force is given by the cross product of vectors i and B multiplied by the length of the wire.
The magnitude of F is given by
F = L i B sin(theta) (from the magnitude of cross product)
If B is perpendicular to the wire, the above simplifies to
F = L i B
Example 1
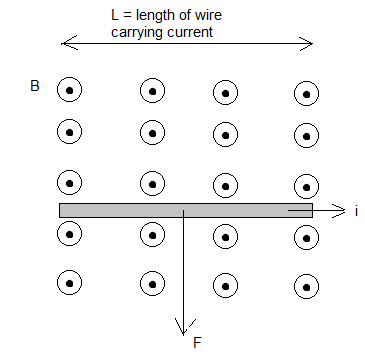
In the figure below, a magnetic field B out of the page exerts a force F (downward) on the current directed to the left. Again the right hand rule was used to find the direction of F as follows:
- Point the index finger in the direction of the current i
- Point the middle finger in the direction of the magnetic field B
and the thumb gives the direction of the force F.
Example 2
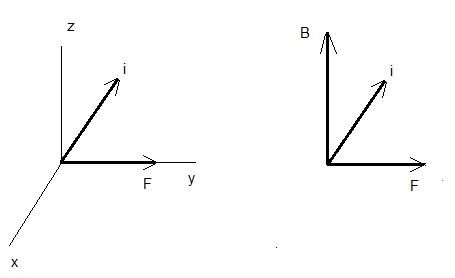
A wire of length 150 cm carrying an electric current of 0.1 A in the negative x direction and perpendicular to a magnetic field B, experiences a force of 6.0 × 10-3 N in the positive y direction due to a magnetic field. Find a) the magnitude and b) direction of the magnetic field.
Solution:
a)
The magnitude may be found by using the formula
F = L i B sin(θ)
where L is the length given as 1.5 meters, i also given as 0.1 A and the magnitude of force F equal to 6.0 × 10-3 N. Angle θ between i and B also given and equal to 90°. Hence
B = F / (L i sin(90°) = 6.0 × 10-3 N / (1.5 × m × 0.1 A) = 4.0 × 10-2 T
b) To find the direction, we first draw the vectors i and F representing the current and the force F as shown on the left. Then apply the right hand rule twice once with B upward and once with B downward and the one that correspond to the right hand rule (index in the direction of i, middle finger in the direction of B and the thumb gives the direction of F). The result is shown on the right.(see figure below).