A positively charged particle moves at a velocity $\mathbf{v}$ perpendicular to a magnetic field $\mathbf{B}$. If the magnitude of the velocity $v$ is doubled, then the magnitude of the force $F$ acting on the moving charge is
A) halved
B) doubled
C) quadrupled
D) quartered
E) not changed
Solution
The magnitude of the force exerted on the particle is given by the Lorentz force equation:
$F = q v B \sin\theta$
For perpendicular motion ($\theta = 90^\circ$), $\sin\theta = 1$, so:
$F = q v B$
Let $v' = 2v$ (doubled). The new force $F'$ is given by:
$F' = q (2v) B = 2 (q v B) = 2F$
The force has doubled.
Answer: B
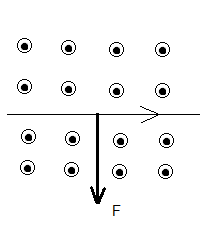
What is the direction of the force acting on a negatively charged particle moving from East to West in a magnetic field directed downward?
A) directed to the right
B) directed to the left
C) directed upward
D) directed into the page
E) directed out of the page
Solution
Using the right-hand rule for positive charges: index finger in the direction of motion (East to West), middle finger in the direction of the magnetic field (downward). For a positive charge, the thumb points out of the page.
However, because the particle has a negative charge, the force direction is reversed: into the page.
Answer: D
A negatively charged particle $q$ enters from the left an area with both an electric field directed downward and a magnetic field of magnitude $6.0 \times 10^{-6} \text{ T}$ directed into the page (see figure below). What must be the magnitude of the electric field so that the particle is not deflected if the magnitude of its velocity is $2.0 \times 10^{5} \text{ cm/s}$?
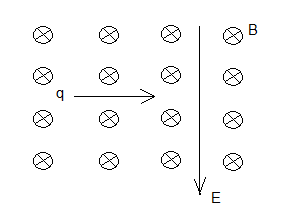
A) 1.2 V/m
B) $3.3 \times 10^{-11} \text{ V/m}$
C) $1.2 \times 10^{-2} \text{ V/m}$
D) $3.3 \times 10^{10} \text{ V/m}$
E) 120 V/m
Solution
On entering the area with electric and magnetic fields, two forces act on the particle:
- Electric force: $\mathbf{F}_e = q\mathbf{E}$ (upward, since $q$ is negative and $\mathbf{E}$ is downward)
- Magnetic force: $\mathbf{F}_m = q\mathbf{v} \times \mathbf{B}$ (downward, by right-hand rule for negative charge)
The particle is not deflected when these forces balance: $F_e = F_m$
$|q|E = |q| v B \Rightarrow E = vB$
Convert velocity to consistent units (m/s):
$v = 2.0 \times 10^{5} \text{ cm/s} = 2.0 \times 10^{3} \text{ m/s}$
Calculate $E$:
$E = (2.0 \times 10^{3} \text{ m/s}) \times (6.0 \times 10^{-6} \text{ T}) = 1.2 \times 10^{-2} \text{ V/m}$
Answer: C
Which of the following diagrams represents the directions of the forces acting on the two wires with current $I$ flowing in the same direction as shown below?
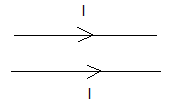
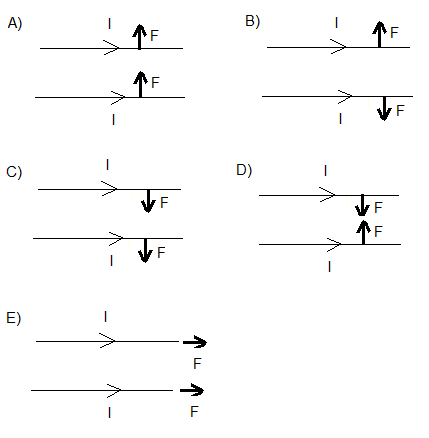
Solution
Step 1: Determine the magnetic field produced by the lower wire at the location of the upper wire using the right-hand grip rule.
Step 2: Apply the right-hand rule to find the force on the upper wire. The field at the upper wire is out of the page. Point index finger in current direction (right), middle finger out of page → thumb points downward.
Step 3: By Newton's Third Law and symmetry, the wires attract each other.
Answer: D
If a force $\mathbf{F}$ is exerted on a charged particle when the particle enters a magnetic field $\mathbf{B}$ at a velocity $\mathbf{v}$, which of the following is always true?
A) Vectors $\mathbf{F}$, $\mathbf{B}$ and $\mathbf{v}$ are all perpendicular to each other
B) Vectors $\mathbf{F}$ and $\mathbf{B}$ are parallel
C) Vectors $\mathbf{F}$ and $\mathbf{B}$ are perpendicular
D) Vectors $\mathbf{F}$ and $\mathbf{v}$ are parallel
E) Vectors $\mathbf{B}$ and $\mathbf{v}$ may be perpendicular
Solution
The force $\mathbf{F}$ exerted on a moving charged particle in a magnetic field is given by:
$\mathbf{F} = q \mathbf{v} \times \mathbf{B}$ (cross product of vectors)
By properties of the cross product, $\mathbf{F}$ is perpendicular to both $\mathbf{v}$ and $\mathbf{B}$.
$\mathbf{v}$ and $\mathbf{B}$ may or may not be perpendicular, but if they are parallel, the force is zero. Therefore, the only statement always true (when $\mathbf{F} \neq \mathbf{0}$) is that $\mathbf{F}$ and $\mathbf{B}$ are perpendicular.
Answer: C
If a magnetic field $\mathbf{B}$ exerts a force $\mathbf{F}$ on a wire of length $L$ with electric current in a magnetic field, then what value of the angle between the direction of the current $i$ and the magnetic field $\mathbf{B}$ gives a maximum value for the magnitude of $F$?
A) $180^\circ$
B) $45^\circ$
C) $90^\circ$
D) $120^\circ$
E) $0^\circ$
Solution
The force $\mathbf{F}$ exerted on a wire in a magnetic field is given by:
$\mathbf{F} = I \mathbf{L} \times \mathbf{B}$ (cross product of vectors)
The magnitude of $F$ is given by:
$F = I L B \sin\theta$ where $\theta$ is the angle between the direction of $I$ (or $\mathbf{L}$) and $\mathbf{B}$.
The maximum value is obtained when $\sin\theta = 1$, i.e., $\theta = 90^\circ$.
Answer: C
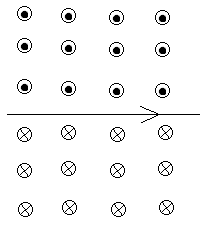
What is the direction of the current that experiences the force $\mathbf{F}$ of a magnetic field $\mathbf{B}$ shown in the diagram below?
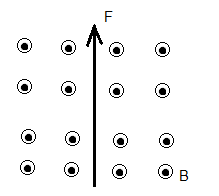
A) Upward
B) Into the page
C) Downward
D) From left to right
E) From right to left
Solution
Apply the right-hand rule: middle finger in the direction of $\mathbf{B}$ (into the page), thumb in the direction of the force $\mathbf{F}$ (upward), and index finger gives the current direction: from right to left.
Answer: E
In the diagram below, wire PQ is part of the closed circuit and is in a magnetic field $\mathbf{B}$. If we neglect the resistance of the wires and the internal resistance of the battery, which of the following is true about the magnitude of the force acting on the wire PQ?
(I) It is proportional to the magnitude of the magnetic field $B$
(II) It is inversely proportional to $R$
(III) It is inversely proportional to $\mathcal{E}$
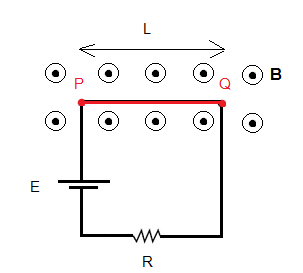
A) (I) only
B) (I), (II) and (III)
C) (I) and (III) only
D) (I) and (II) only
E) (II) and (III) only
Solution
The magnitude of force $F$ on a current-carrying wire PQ is given by:
$F = I L B$, where $I$ is the current in the circuit.
From Ohm's Law: $I = \dfrac{\mathcal{E}}{R}$
Hence $F = L \cdot \dfrac{\mathcal{E}}{R} \cdot B = \dfrac{L \mathcal{E} B}{R}$
$F$ is proportional to $B$, proportional to $\mathcal{E}$, and inversely proportional to $R$.
Thus (I) and (II) are true, but (III) is false.
Answer: D
Two parallel wires with the same current $I$ exert forces on each other with equal magnitudes. What happens to the magnitude of this force if the current is halved?
A) The magnitude is quartered
B) The magnitude is halved
C) The magnitude is doubled
D) The magnitude is quadrupled
E) The magnitude does not change
Solution
The magnitude of force $F$ on a current-carrying wire of length $L$ due to another parallel wire is given by:
$F = I L B$, where $B$ is the magnetic field produced by the second wire.
The magnitude of the magnetic field $B$ due to a current-carrying wire (second wire) at distance $r$ is:
$B = \dfrac{\mu_0 I}{2\pi r}$
Substituting $B$ into $F$:
$F = I L \cdot \dfrac{\mu_0 I}{2\pi r} = \dfrac{\mu_0 I^2 L}{2\pi r}$
If $I$ is halved ($I' = I/2$), then the new force is:
$F' = \dfrac{\mu_0 (I/2)^2 L}{2\pi r} = \dfrac{1}{4} \cdot \dfrac{\mu_0 I^2 L}{2\pi r} = \dfrac{F}{4}$
The force is quartered.
Answer: A
In the circuit below wire PQ, with mass of 10 grams and length of 20 cm, can move up and down with negligible friction. If a uniform magnetic field $\mathbf{B}$ of magnitude 1 T and direction out of the page is applied to wire PQ, what must be the direction and the smallest intensity of the current in the circuit that lifts wire PQ upward?
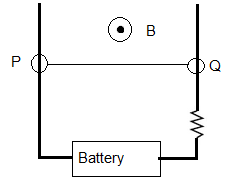
A) Direction: from Q to P, Minimum intensity: 2 A
B) Direction: from P to Q, Minimum intensity: 0.5 A
C) Direction: from P to Q, Minimum intensity: 2 A
D) Direction: from Q to P, Minimum intensity: 1 A
E) Direction: from Q to P, Minimum intensity: 0.5 A
Solution
The magnetic field exerts a force $\mathbf{F}$ on the current-carrying wire PQ. For the force to lift the wire, $\mathbf{F}$ must be directed upward and its magnitude must be at least equal to the weight of the wire (since friction is negligible).
Using the right-hand rule: middle finger in the direction of $\mathbf{B}$ (out of page), thumb in the direction of force (upward), the index finger points from right to left → current direction from Q to P.
The magnitude of force $F$ on the wire is:
$F = I L B = (0.2 \text{ m}) \cdot I \cdot (1 \text{ T})$
Require $F \geq mg$, where $m = 0.01 \text{ kg}$ and $g = 10 \text{ m/s}^2$:
$0.2 I \geq (0.01 \text{ kg}) \times (10 \text{ m/s}^2)$
$I \geq 0.5 \text{ A}$
Minimum current is 0.5 A, direction from Q to P.
Answer: E