Solutions to the problems on displacement and distance of moving objects.
Problem 1
An object moves from point A to point B to point C, then back to point B and then to point C along the line shown in the figure below.
a) Find the distance covered by the moving object.
b) Find the magnitude and direction of the displacement of the object.
Solution to Problem 1:
a) distance = AB + BC + CB + BC = 5 + 4 + 4 + 4 = 17 km
b) The magnitude of the displacement is equal to the distance between the final point C and the initial point A = AC = 9 km
The direction of the displacement is the direction of the ray AB.
Problem 2
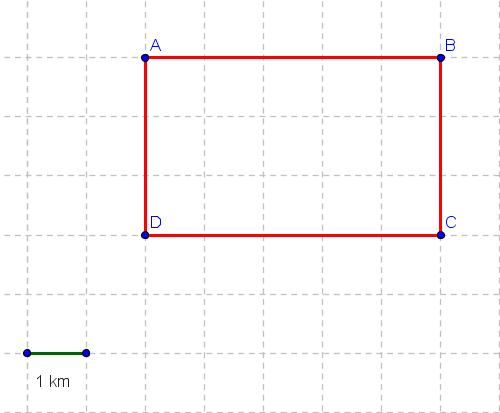
An object moves from point A to point C along the rectangle shown in the figure below.
a) Find the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
Solution to Problem 2:
a) distance = AB + BC = 5 + 3 = 8 km
b) Initial point is A and the final point is C, hence the magnitude of the displacement is equal the diagonal AC of the rectangle and is calculated using Pythagora's theorem as follows
AC2 = AB2 + BC2 = 52 + 32 = 25 + 9 = 34
AC = √34 km
Problem 3
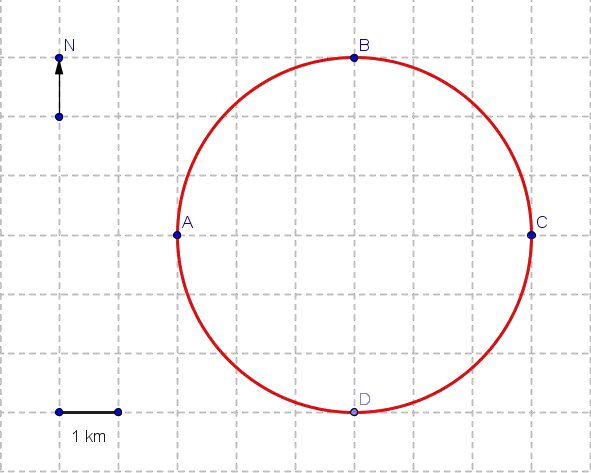
An object moves from point A to B to C to D and finally to A along the circle shown in the figure below.
a) Find the distance covered by the moving object.
b) Find the magnitude and direction of the displacement of the object.
Solution to Problem 3:
a) The object moves one complete rotation and therefore the distance d is equal to the circumference and is given by
d = 2 Pi * radius = 6 Pi km
b) Initial point is A and the final point is A, no change in position; hence the magnitude of the displacement is equal to zero
Problem 4
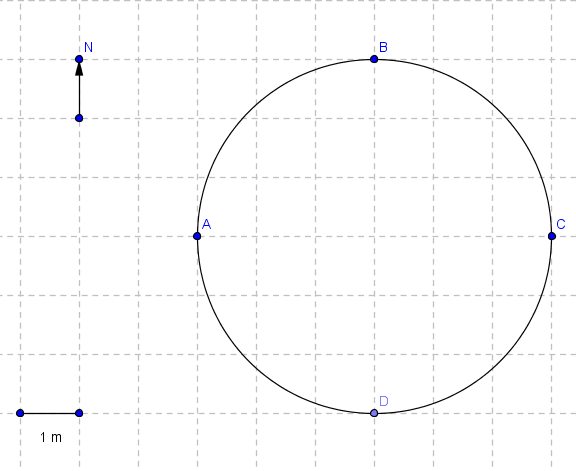
An object moves from point A to B to C to D along the circle shown in the figure below.
a) Find the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
Solution to Problem 4:
a) The object moves 3/4 of one rotation and therefore the distance d is equal to 3/4 of the circumference and is given by
d = (3/4) (2 Pi * radius) = 4.5 Pi m
b) Initial point is A and the final point is D, hence the magnitude of the displacement is equal to the distance AD which is calculated using Pythagora's theorem to the triangle AOD as shown in the figure below
AD2 = AO2 + OD2 = 32 + 32 = 18
magnitude of displacement = AD = 3√2 m
Problem 5
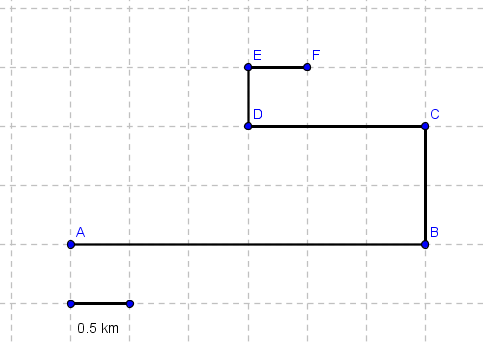
An object moves along the grid through the points A, B, C, D, E, and F as shown below.
a) Find the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
Solution to Problem 5:
a) distance = AB + BC + CD + DE + EF = 3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 km
b) Initial point is A and the final point is F, hence the magnitude of the displacement is equal to the distance AF which is calculated by applying Pythagora's theorem to the triangle AHF as shown in the figure below
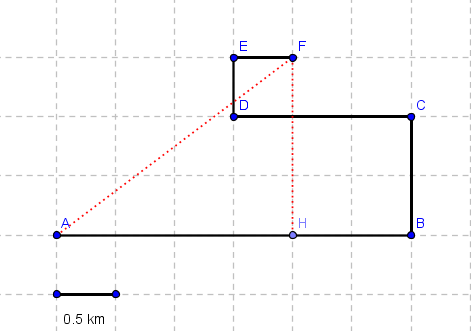
AF2 = AH2 + HF2 = (0.5*4)2 + (0.5*3)2 = 4 + 2.25 = 6.25
magnitude of displacement = AF = 2.5 km