Solutions to the problems on velocity and speed of moving objects. More tutorials can be found in this website.
Problem 1:
A man walks 7 km in 2 hours and 2 km in 1 hour in the same direction.
a) What is the man's average speed for the whole journey?
b) What is the man's average velocity for the whole journey?
Solution to Problem 1:
a)
|
average speed =
|
distance
time
|
=
|
7 km + 2 km
2 hours + 1 hour
|
=
|
9 km
3 hours
|
= 3 km/h |
|
average velocity =
|
displacement
time
|
=
|
7 km + 2 km
2 hours + 1 hour
|
=
|
9 km
3 hours
|
= 3 km/h |
Problem 2:
A man walks 7 km East in 2 hours and then 2.5 km West in 1 hour.
a) What is the man's average speed for the whole journey?
b) What is the man's average velocity for the whole journey?
Solution to Problem 2:
a)
|
average speed =
|
distance
time
|
=
|
7 km + 2.5 km
2 hours + 1 hour
|
=
|
9.5 km
3 hours
|
= 3.2 km/h (approximated to the nearest tenth) |
|
average velocity =
|
displacement
time
|
=
|
7 km - 2.5 km
2 hours + 1 hour
|
=
|
4.5 km
3 hours
|
= 1.5 km/h |
Problem 3:
You start walking from a point on a circular field of radius 0.5 km and 1 hour later you are at the same point.
a) What is your average speed for the whole journey?
b) What is your average velocity for the whole journey?
Solution to Problem 3:
a)
If you walk around a circular field and come back to the same point, you have covered a distance equal to the circumference of the circle.
|
average speed =
|
distance
time
|
=
|
circumference
time
|
=
|
2 * 0.5 * Pi
1 hour
|
= Pi km/h = 3.14 km/h (approximated) |
Problem 4:
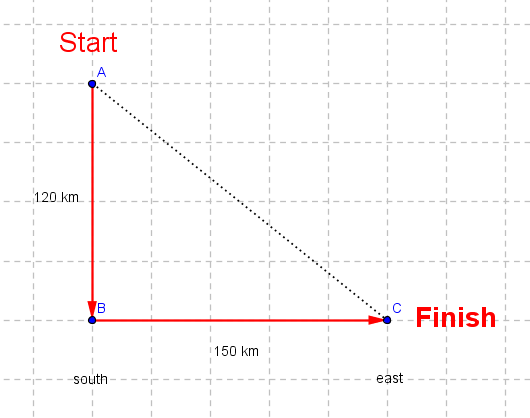
John drove South 120 km at 60 km/h and then East 150 km at 50 km/h. Determine
a) the average speed for the whole journey?
b) the magnitude of the average velocity for the whole journey?
Solution to Problem 4:
a)
t1 = 120 / 60 = 2 hours
The time t2 to cover 150 km at a speed of 50 km/h is given by
t2 = 150 / 50 = 3 hours
|
average speed =
|
distance
time
|
=
|
120 km + 150 km
2 hours + 3 hours
|
=
|
270 km
5 hours
|
= 54 km/h |
AC 2 = 120 2 + 150 2 AC = √(14400+22500) = 30 √41 km
|
average velocity =
|
displacement
time
|
=
|
30 √41 km
2 hours + 3 hour
|
= 38.4 km/h (approximated) |
Problem 5:
If I can walk at an average speed of 5 km/h, how many miles I can walk in two hours?
Solution to Problem 5:
distance = (average speed) * (time) = 5 km/h * 2 hours = 10 km
using the rate of conversion 0.62 miles per km, the distance in miles is given by
distance = 10 km * 0.62 miles/km = 6.2 miles
Problem 6:
A train travels along a straight line at a constant speed of 60 mi/h for a distance d and then another distance equal to 2d in the same direction at a constant speed of 80 mi/h.
a)What is the average speed of the train for the whole journey?
Solution to Problem 6:
a) The time t1 to cover distance d at a speed of 60 mi/h is given by
t1 = d / 60
The time t2 to cover distance 2d at a speed of 80 mi/h is given by
t2 = 2d / 80
|
average speed =
|
distance
time
|
=
|
d + 2d
d/60 + 2d/80
|
=
|
3d
(80d + 2d*60)/(60*80)
|
=
|
3d
200d/4800
|
=
|
3d*4800
200d
|
= 72 mi/h |
Problem 7:
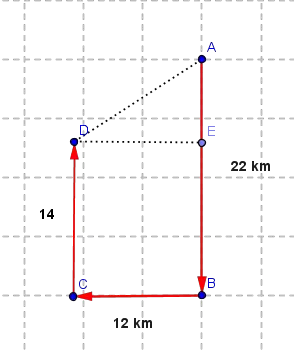
A car travels 22 km south, 12 km west, and 14 km north in half an hour.
a) What is the average speed of the car?
b) What is the final displacement of the car?
c) What is the average velocity of the car?
|
average speed =
|
distance
time
|
=
|
22 km + 12 km + 14 km
0.5 hour
|
= 96 km/h |
AE = 22 - 14 = 8 km
DA 2 = AE 2 + ED 2 = 8 2 + 12 2 = 64 + 144 = 208
DA = √208 = 4√13 km
c)
|
average velocity =
|
displacement
time
|
=
|
4√13 km
0.5 hour
|
= 28.8 km/h (approximated) |
Problem 8: A man walked from point A to F following the route in the grid below in 3250 seconds. Determine
b) the magnitude of the displacement.
c) the magnitude of the average velocity, in m/s, for the whole journey.
|
average speed =
|
distance
time
|
=
|
3 km + 1 km + 1.5 km + 0.5 km + 0.5 km
3250 seconds
|
=
|
6.5 km
3250 seconds
|
=
|
6500 m
3250 seconds
|
= 2 m/s |
AF 2 = FH 2 + HA 2 = 3 2 + 4 2 = 9 + 16 = 25
DA = √25 = 5 km
c)
|
average velocity =
|
displacement
time
|
=
|
5 km
3250 s
|
=
|
5000 m
3250 s
|
= 1.5 m/s (approximated) |