Examples with explanations on the concepts of average speed and average velocity of moving object. More problems and their solutions can be found in this website.
Average Speed and Average Velocity Definitions
The average speed is a scalar quantity (magnitude) that describes the rate of change (with the time) of the distance of a moving object.
|
average speed =
|
distance
time
|
The average velocity is a vector quantity (magnitude and direction) that describes the rate of change (with the time) of the position of a moving object.
|
average velocity =
|
change in position
time
|
=
|
displacement
time
|
Examples with Detailed Solutions
Example 1:
An object moves from A to D along the red path as shown below in 41 minutes and 40 seconds.
a) Find the average speed of the object in m/s
b) Find the average velocity of the object in m/s
a) Using the given scale (1km per division); the total distance d is given by
d = AB + BC + CD = 2 + 5 + 2 = 9 km
|
average speed =
|
distance
time
|
=
|
9 km
41 mn + 40 s
|
=
|
9000 m
(41*60 + 40) s
|
=
|
9000 m
2500 s
|
= 3.6 m/s |
b) The final and initial and positions of the moving object are used to find the displacement. The distance from A (initial position) to D (final position) is equal to AD = 5 km. The displacement is the vector AD whose magnitude if 5 km and its direction is to the east.
|
average velocity =
|
displacement
time
|
=
|
5 km
41 mn + 40 s
|
=
|
5000 m
2500 s
|
= 2.5 m/s |
The average velocity is a vector whose magnitude is 2.5 m/s and its direction is to the east.
Example 2:
An object moves, along a line, from point A to B to C and then back to B again as shown in the figure below in half an hour.
a) Find the average speed of the moving object in km/h.
b) Find the magnitude of the average velocity of the object in km/h.
a) The total distance d covered by the object is
d = AB + BC + CB = 5 km + 4 km + 4 km = 13 km
|
average speed =
|
distance
time
|
=
|
13 km
0.5 hour
|
= 26 km/h |
|
average velocity =
|
displacement
time
|
=
|
5 km
0.5 hour
|
= 10 km/h |
Example 3:
An fast object moves from point A to B to C to D and then back to A along the rectangle shown in the figure below in 5 seconds.
a) Find the average speed of the moving object in m/s.
b) Find the velocity of the object in m/s.
a) The total distance d is equal to the perimeter of the rectangle. Using the given scale,
d = 2 AB + 2 BC = 10 + 6 = 16 km
|
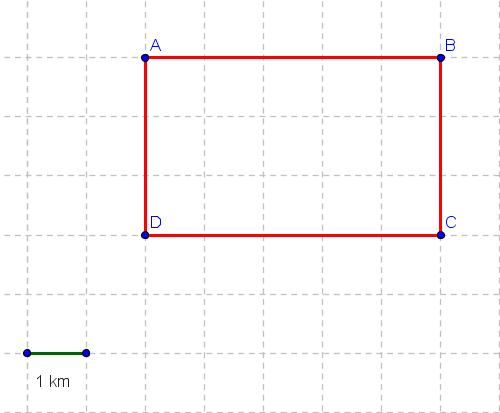
average speed =
|
distance
time
|
=
|
16 km
5 seconds
|
=
|
16000 m
5 seconds
|
= 3200 m/s |
|
average velocity =
|
displacement
time
|
=
|
0
5 second
|
= 0 |
Example 4:
A person walks, for two hours, from point A to B to C along a circular field as shown in the figure below.
a) Find the average speed of the person in km/h.
b) Find the velocity of the person.
a) The total distance d is equal to half the circumference of the circle and given by
d = (1/2)(2 * Pi * 3) = 3 Pi
|
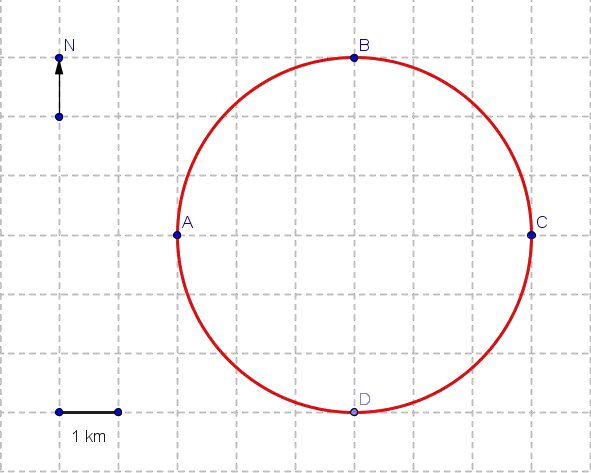
average speed =
|
distance
time
|
=
|
3 Pi km
2 hours
|
= 1.5 Pi km/h = 4.7 km/h |
b) The magnitude of the displacement D is equal to the diameter AC of the circle and is given by
D = 2 * 3 = 6 Km with direction to the East
|
average velocity =
|
displacement
time
|
=
|
6 km
2 hours
|
= 3 km/h |
Example 5:
A person walks for one hour and 12 minutes, from point A to point B, along a circular field as shown in the figure.
a) Find the average speed of the person in km/h.
b) Find the magnitude of the displacement of the person in km/h.
a) The total distance d is equal to the quarter the circumference of the circle and given by
d = (1/4)(2 * Pi * 3) = 1.5 Pi
|
average speed =
|
distance
time
|
=
|
1.5 Pi km
1 hour + 12 minutes
|
=
|
1.5 Pi km
1 hour + 12/60 hour
|
=
|
1.5 Pi km
1.2 hour
|
= 1.25 Pi km/h = 3.9 km/h
b) The magnitude of the displacement D is equal to the hypotenuse AB of the right angle ABO as shown below
AB 2 = 3 2 + 3 2 = 18
D = AB = 3√2 km
|
average velocity =
|
displacement
time
|
=
|
3√2 km
1 hour + 12 minutes
|
=
|
3√2 km
1.2 hours
|
= 2.5√2 km/h = 3.5 km/h
