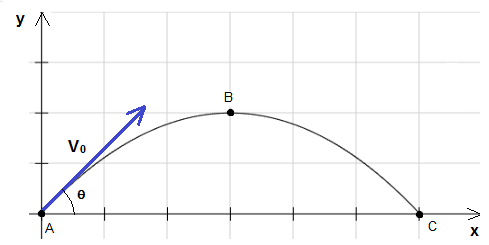
Consider a projectile being launched at an initial velocity v0 in a direction making an angle θ with the horizontal. We assume that air resistance is negligible and the only force acting on the object is the force of gravity with acceleration g = 9.8 m/s2. Also an interactive html 5 applet may be used to better understand the projectile equations. Projectile problems with solutions are also included in this site.

The initial velocity V0 being a vector quantity, has two components:
V0x and V0y given by
V0x = V0 cos(θ)
V0y = V0 sin(θ)
The acceleration A is a also a vector with two components Ax and Ay given by
Ax = 0 and Ay = - g = - 9.8 m/s2
Along the x axis the acceleration is equal to 0 and therefore the velocity Vx is constant and is given by
Vx = V0 cos(θ)
Along the y axis, the acceleration is uniform and equal to - g and the velocity at time t is given by
Vy = V0 sin(θ) - g t
Along the x axis the velocity Vxis constant and therefore the component x of the displacement is given by
x = V0 cos(θ) t
Along the y axis, the motion is that of a uniform acceleration type and the y component of the displacement is given by
y = V0 sin(θ) t - (1/2) g t2
The shape of the trajectory followed by the projectile is found as follows
Solve the formula \( \; x = V_0 cos(\theta) t \; \) for \( t \) to obtain
\[ t = \dfrac{x}{V_0 cos(\theta)} \]
Substitute \( t \) by \( \dfrac{x}{V_0 cos(\theta)} \) in the above expression of y to obtain
\[ y = \dfrac{V_0 \sin(\theta) x}{V_0 \cos(\theta)} - (1/2) g \left( \dfrac{x}{V_0 \cos(\theta)} \right)^2 \]
Simplify
\[ y = - \dfrac{g \; x^2}{2( V_0 \cos(\theta))^2} + x \tan(\theta) \]
The above equation is the path of projectile which is a parabola of the form
\( y = A x^2 + B x \)
where \( A = - \dfrac{g}{2( V_0 \cos(\theta))^2} \) and \( B = \tan(\theta) \)
The time of flight is the time taken for the projectile to go from point
A to point C (see figure above).
It is calculated by setting y = 0 (y = 0 at point C) and solve for t
y = V0 sin(θ) t - (1/2) g t2 = 0
Factor t out in the above equation
t(V0 sin(θ) - (1/2) g t) = 0
Two solutions:
t = 0 (correspond to point A)
and
t = 2 V0 sin(θ) / g (correspond to point C)
Hence the time of flight = 2 V0 sin(θ) / g
At point B in the figure above, the projectile is momentarily horizontal and therefore the vertical component of its velocity is equal to zero. Hence
Vy = V0 sin(θ) - g t = 0
Solve for t to obtain
t = V0 sin(θ) / g (Note: this is half the time of flight because of the symmetry of the parabola)
Substitute t by V0 sin(θ) / g in the expression of y, we obtain the maximum height
\( H = \dfrac{V_0 \sin(\theta) V_0 sin(\theta)}{g} - (1/2) \dfrac{}{} g \left( \dfrac{V_0 sin(\theta)}{g} \right)^2 = \dfrac{(V_0 sin(\theta))^2}{2 g} \)
Distance AC which is the horizontal range is equal to x when t is equal to the time of flight 2 V0 sin(θ) / g obtained above. Hence
range AC = x = V0 cos(θ) t at t = time of flight = 2 V0 sin(θ) / g
Substitute t by 2 V0 sin(θ) / g and simplify to obtain the range AC
AC \( = V_0 cos(\theta) 2 V_0 sin(\theta) / g = V_0^2 sin(2\theta) / g \)