Solutions and detailed explanations to projectile problems are presented . These solutions may be better understood when projectile equations are first reviewed.

Detailed Solutions

Problem 1

An object is launched at a velocity of 20 m/s in a direction making an angle of 25° upward with the horizontal.
a) What is the maximum height reached by the object?
b) What is the total flight time (between launch and touching the ground) of the object?
c) What is the horizontal range (maximum x above ground) of the object?
d) What is the magnitude of the velocity of the object just before it hits the ground?

Solution to Problem 1:

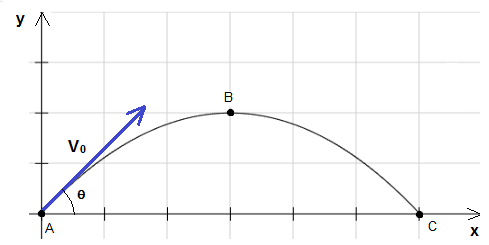
a) The formulas for the components V_x and V_y of the velocity and components x and y of the displacement are given by
V_x = V₀ cos(θ)       V_y = V₀ sin(θ) - g t
x = V₀ cos(θ) t       y = V₀ sin(θ) t - (1/2) g t²
In the problem V₀ = 20 m/s, θ = 25° and g = 9.8 m/s².
The height of the projectile is given by the component y, and it reaches its maximum value when the component V_y is equal to zero. That is when the projectile changes from moving upward to moving downward.(see figure above) and also the animation of the projectile.
V_y = V₀ sin(θ) - g t = 0
solve for t
t = V₀ sin(θ) / g = 20 sin(25°) / 9.8 = 0.86 seconds
Find the maximum height by substituting t by 0.86 seconds in the formula for y
maximum height y (0.86) = 20 sin(25°)(0.86) - (1/2) (9.8) (0.86) ² = 3.64 meters
b) The time of flight is the interval of time between when projectile is launched: t1 and when the projectile touches the ground: t2. At t = t1 and t = t2, y = 0 (ground). Hence
V₀ sin(θ) t - (1/2) g t² = 0
Solve for t
t(V₀ sin(θ) - (1/2) g t) = 0
two solutions
t = t1 = 0 and t = t2 = 2 V₀ sin(θ) / g
Time of flight = t2 - t1 = 2 (20) sin(θ) / g = 1.72 seconds.
c) In part c) above we found the time of flight t2 = 2 V₀ sin(θ) / g. The horizontal range is the horizontal distance given by x at t = t2.
range = x(t2) = V₀ cos(θ) t2 = 2 V₀ cos(θ) V₀ sin(θ) / g = V₀² sin(2θ) / g = 20² sin (2(25°)) / 9.8 = 31.26 meters

d) The object hits the ground at t = t2 = 2 V0 sin(θ) / g (found in part b above)
The components of the velocity at t are given by
V_x = V₀ cos(θ)       V_y = V₀ sin(θ) - g t
The components of the velocity at t = 2 V0 sin(θ) / g are given by
V_x = V₀ cos(θ) = 20 cos(25°)       V_y = V₀ sin(25°) - g (2 V0 sin(25°) / g) = - V₀ sin(25°)
The magnitude V of the velocity is given by
V = √[ V_x² + V_y² ] = √[ (20 cos(25°))² + (- V₀ sin(25°))² ] = V0 = 20 m/s

Problem 2

A projectile is launched from point O at an angle of 22° with an initial velocity of 15 m/s up an incline plane that makes an angle of 10° with the horizontal. The projectile hits the incline plane at point M.
a) Find the time it takes for the projectile to hit the incline plane.
b)Find the distance OM.

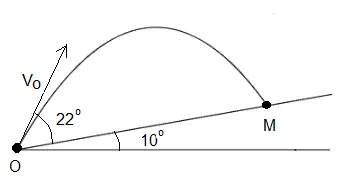
Solution to Problem 2:
a) The x and y components of the displacement are given by
x = V₀ cos(θ) t       y = V₀ sin(θ) t - (1/2) g t²
with θ = 22 + 10 = 32° and V₀ = 15 m/s
The relationship between the coordinate x and y on the incline is given by
tan(10°) = y / x
Substitute x and y by their expressions above to obtain
tan(10°) = ( V₀ sin(θ) t - (1/2) g t²) / V₀ cos(θ) t
Simplify to obtain the equation in t
(1/2) g t + V₀ cos(θ) tan(10°) - V₀ sin(θ) = 0
Solve for t

Problem 3

A projectile is to be launched at an angle of 30° so that it falls beyond the pond of length 20 meters as shown in the figure.
a) What is the range of values of the initial velocity so that the projectile falls between points M and N?

Solution to Problem 3:
a) The range is given by x = V₀² sin(2θ) / g
We want to have the range greater than OM and smaller that ON, with OM = 10 + 20 = 30 m and ON = 10 + 20 + 10 = 40 m
30 < V₀² sin(2θ) / g < 40
30 g / sin(2θ) < V₀² < 40 g / sin(2θ)
√ [ 30 g / sin(2θ) ] < V₀ < √ [ 40 g / sin(2θ) ]
18.4 m/s < V₀² < 21.2 m/s

Problem 4

A ball is kicked at an angle of 35° with the ground.
a) What should be the initial velocity of the ball so that it hits a target that is 30 meters away at a height of 1.8 meters?
b) What is the time for the ball to reach the target?

Solution to Problem 4:
a)
x = V₀ cos(35°) t
30 = V₀ cos(35°) t
t = 30 / V₀ cos(35°)
1.8 = -(1/2) 9.8 (30 / V₀ cos(35°))² + V₀ sin(35°)(30 / V₀ cos(35°))
V₀ cos(35°) = 30 √ [ 9.8 / 2(30 tan(35°)-1.8) ]
V₀ = 18.3 m/s
b)
t = x / V₀ cos(35°) = 2.0 s

Problem 5

A ball kicked from ground level at an initial velocity of 60 m/s and an angle θ with ground reaches a horizontal distance of 200 meters.
a) What is the size of angle θ?
b) What is time of flight of the ball?

Solution to Problem 5:
a)
Let T be the time of flight. Two ways to find the time of flight
1) T = 200 / V₀ cos(θ) (range divided by the horizontal component of the velocity)
2) T = 2 V₀ sin(θ) / g (formula found in projectile equations)
equate the two expressions
200 / V₀ cos(θ) = 2 V₀ sin(θ) / g
which gives
2 V₀² cos(θ)sin (θ) = 200 g
V₀² sin(2θ) = 200 g
sin(2θ) = 200 g / V₀² = 200 (9.8) / 60²
Solve for θ to obtain
θ = 16.5°
b)
Time of flight = 200 / V₀ cos(16.5°) = 3.48 s

Problem 6

A ball of 600 grams is kicked at an angle of 35° with the ground with an initial velocity V₀.
a) What is the initial velocity V₀ of the ball if its kinetic energy is 22 Joules when its height is maximum?
b) What is the maximum height reached by the ball

Solution to Problem 6:
a)
When the height of the ball is maximum, the vertical component of its velocity is zero; hence the kinetic energy is due to its horizontal component V_x = V₀ cos (θ).
22 = (1/2) m (V_x)²
22 = (1/2) 0.6 (V₀ cos (35°))²
V₀ = (1 / cos (35°)) √(44/0.6) = 10.4 m/s
b)
Initial kinetic energy (just after the ball is kicked)
E_i = (1/2) m V₀² = (1/2) 0.6 (10.4)² = 32.4 J
The difference between initial kinetic energy and kinetic energy when the ball is at maximum height H is equal to gain in potential energy
32.4 - 22 = m g H
H = 10.4 / (0.6 * 9.8) = 1.8 m

Problem 7

A projectile starting from ground hits a target on the ground located at a distance of 1000 meters after 40 seconds.
a) What is the size of the angle θ?
b) At what initial velocity was the projectile launched?

Solution to Problem 7:
a)
Vx = V₀ cos (θ) = 1000 / 40 = 25 m/s
Time of flight = 2 V₀ sin (θ) / g (formula found in projectile equations)
= 40 s
V₀ sin (θ) = 20 g
Combine the above equation with the equation V₀ cos (θ) = 25 m/s found above to write
tan (θ) = 20 g / 25
Use calculator to find θ = 82.7 °
b)
We now use any of the two equations above to find V₀.
V₀ cos (θ) = 25 m/s
V₀ = 25 /cos (82.7 °) = 196.8 m/s

Problem 8

The trajectory of a projectile launched from ground is given by the equation y = -0.025 x² + 0.5 x, where x and y are the coordinate of the projectile on a rectangular system of axes.
a) Find the initial velocity and the angle at which the projectile is launched.

Solution to Problem 8:
a)
y = tan(θ) x - (1/2) (g / (V₀ cos (θ))² ) x² (formula found in projectile equations)
hence tan(θ) = 0.5 which gives θ = arctan(0.5) = 26.5 °
-0.025 = -0.5 (9.8 / (V₀ cos (26.5 °))² )
Solve for V₀ to obtain V₀ = 15.6 m/s

Problem 9

Two balls A and B of masses 100 grams and 300 grams respectively are pushed horizontally from a table of height 3 meters. Ball has is pushed so that its initial velocity is 10 m/s and ball B is pushed so that its initial velocity is 15 m/s.
a) Find the time it takes each ball to hit the ground.
b) What is the difference in the distance between the points of impact of the two balls on the ground?

Solution to Problem 9:
a) The two balls are subject to the same gravitational acceleration and therefor will hit the ground at the same time t found by solving the equation
-3 = -(1/2) g t²
t = √ (3(2)/9.8) = 0.78 s
b) Horizontal distance XA of ball A
XA = 10 m/s * 0.78 s = 7.8 m
Horizontal distance XB of ball B
XB = 15 m/s * 0.78 s = 11.7 m
Difference in distance XA and XB is given by
|XB - XA| = |11.7 - 7.8| = 3.9 m

More References and Links

1. Projectile Motion Calculator and Solver
2. Projectile Problems with Solutions and Explanations
3. Solutions and Explanations to Projectile Problems
4. Projectile Equations with Explanations
5. Interactive Simulation of Projectile.