Linear Momentum Questions with Solutions

Linear momentum questions with solutions and explanations are presented. These questions may be used to practice for the SAT physics test.

Questions

  1. If the speed and mass of an object are doubled, which of the following is true?

    A) The momentum of the object is doubled
    B) The kinetic energy of the object is doubled
    C) The momentum of the object is quadrupled
    D) The kinetic energy of the object is multiplied by 8
    E) The momentum and the kinetic energy of the object are quadrupled

  2. Two objects A and B of velocities \( v_1 \) and \( v_2 \) have momenta with equal magnitude. If \( |v_1| < |v_2| \), which of the following is true?

    A) The two objects have equal kinetic energies
    B) The two objects have equal masses
    C) The kinetic energy of A is greater than the kinetic energy of B
    D) The kinetic energy of B is greater than the kinetic energy of A
    E) Mass of object A is greater than mass of object B

  3. Two objects A and B have velocities \( v_1 \) and \( v_2 \) and masses \( m_1 \) and \( m_2 \). If \( |v_1| < |v_2| \) and the two objects have equal kinetic energies, which of the following is true?

    A) The two objects have momenta with equal magnitudes
    B) The magnitude of the momentum of A is greater than the magnitude of the momentum of B
    C) The magnitude of the momentum of A is smaller than the magnitude of the momentum of B
    D) The two objects have equal masses
    E) Mass of object A is smaller than mass of object B

  4. How long does it take a 2000-kg car to stop from a velocity of 35 m/s if a braking force of 4000 Newtons is used?

    A) 35 s
    B) 70 s
    C) 8.75 s
    D) 10 s
    E) 17.5 s

  5. Object A of mass \( m_1 \) is moving at a velocity \( v_1 \) to the right. It collides and sticks to object B of mass \( m_2 \) moving in the same direction as object A with a velocity \( v_2 \). After collision, the two objects have a velocity equal to \( \frac{1}{2}(v_1 + v_2) \). What is the relationship between \( m_1 \) and \( m_2 \)?

    A) \( m_1 > m_2 \)
    B) \( m_1 < m_2 \)
    C) \( m_1 = 2 m_2 \)
    D) \( m_1 = m_2 \)
    E) \( m_1 = \frac{1}{2} m_2 \)

  6. A 2-kilogram object slides, on a smooth surface, towards the north at a velocity of 5 meters per second. The object hits a fixed pole and is deflected from north to east by an angle of 60° and has a velocity of 5 meters per second. The change in the magnitude of the northward component of the momentum of the object is

    A) -15 kg·m/s
    B) -10 kg·m/s
    C) -5 kg·m/s
    D) 0 kg·m/s
    E) 5 kg·m/s

  7. An object of mass 4 kg is moving towards the east at a velocity of 6 meters per second. It collides and sticks to a 6-kg object moving with a velocity of 5 meters per second in the same direction. How much kinetic energy was lost in the collision?

    A) 1.2 J
    B) 4.25 J
    C) 0 J
    D) 2.4 J
    E) 5 J

  8. Two objects A and B of masses 1 and 3 kg are held by a compressed massless spring and are at rest. When the spring is released, object A moves to the left with a velocity of 9 m/s. What is the velocity (magnitude and direction) of object B?

    A) 3 m/s to the left
    B) 3 m/s to the right
    C) 9 m/s to the left
    D) 9 m/s to the right
    E) 4.5 m/s to the left

  9. Which of the following statements is true?

    A) In an elastic collision, only momentum is conserved.
    B) In an inelastic collision, both momentum and kinetic energy are conserved.
    C) In an elastic collision, only kinetic energy is conserved.
    D) In any collision, momentum is conserved.
    E) In any collision, both momentum and kinetic energy are conserved.

  10. An object A of mass \( m_1 \) is moving at a speed \( v_1 \) in a straight line to the right. Another object B of mass \( m_2 \) is moving to the left in the same path as object A but in the opposite direction. What would be the speed of object B be so that when the two objects collide they stick to each other and stop?

    A) \( \frac{m_1 |v_1|}{m_1 + m_2} \)
    B) \( \frac{m_1 |v_1|}{m_2} \)
    C) \( \frac{(m_1 + m_2) |v_1|}{m_1} \)
    D) \( \frac{m_2 |v_1|}{m_1} \)
    E) \( \frac{m_2 |v_1|}{m_1 + m_2} \)

Solutions to Above Questions

  1. \[ p = mv \] \[ K = \frac{1}{2}mv^2 \] Let \( M = 2m \) and \( V = 2v \) (mass and velocity doubled). \[ P = MV = (2m)(2v) = 4mv \] Momentum is quadrupled. \[ K = \frac{1}{2}MV^2 = \frac{1}{2}(2m)(2v)^2 = \frac{1}{2}(8mv^2) \] Kinetic energy is multiplied by 8.
    Answer: D

  2. Equal momenta: \( |p_1| = m_1|v_1| \), \( |p_2| = m_2|v_2| \). Let \( K_1 = \frac{1}{2}m_1|v_1|^2 \), \( K_2 = \frac{1}{2}m_2|v_2|^2 \). Given \( |v_1| < |v_2| \) and \( |p_1| = |p_2| \). Multiply by \( \frac{1}{2}|p_1| = \frac{1}{2}|p_2| \): \[ \frac{1}{2}|p_1||v_1| < \frac{1}{2}|p_2||v_2| \] Substitute: \[ \frac{1}{2}m_1|v_1|^2 < \frac{1}{2}m_2|v_2|^2 \] Thus \( K_1 < K_2 \).
    Answer: D

  3. Equal kinetic energies: \( K_1 = \frac{1}{2}m_1|v_1|^2 = K_2 = \frac{1}{2}m_2|v_2|^2 \). Let \( |p_1| = m_1|v_1| \), \( |p_2| = m_2|v_2| \). Given \( |v_1| < |v_2| \), divide by \( K_1 = K_2 \): \[ \frac{|v_1|}{K_1} < \frac{|v_2|}{K_2} \Rightarrow \frac{K_1}{|v_1|} > \frac{K_2}{|v_2|} \] Substitute: \[ \frac{\frac{1}{2}m_1|v_1|^2}{|v_1|} > \frac{\frac{1}{2}m_2|v_2|^2}{|v_2|} \Rightarrow m_1|v_1| > m_2|v_2| \Rightarrow |p_1| > |p_2| \].
    Answer: B

  4. Using impulse-momentum theorem: \( F\Delta t = \Delta p = m(v_f - v_i) \). Magnitude: \( |F|\Delta t = m|v_f - v_i| \). \[ \Delta t = \frac{2000 \times |0 - 35|}{4000} = 17.5 \text{ seconds} \].
    Answer: E

  5. Momentum conservation: \( m_1v_1 + m_2v_2 = (m_1 + m_2)\frac{1}{2}(v_1 + v_2) \). Multiply by 2: \( 2m_1v_1 + 2m_2v_2 = (m_1 + m_2)(v_1 + v_2) \). Expand and simplify: \( m_1v_1 - m_1v_2 + m_2v_2 - m_2v_1 = 0 \) ⇒ \( (m_1 - m_2)(v_1 - v_2) = 0 \). Since \( v_1 \neq v_2 \), \( m_1 = m_2 \).
    Answer: D

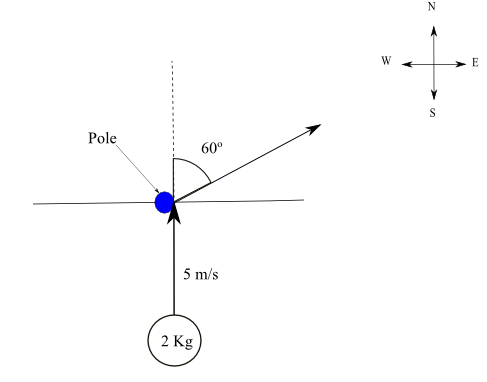
  6. momentum problem question 6
    Initial northward momentum: \( p_{1n} = 2 \times 5 = 10 \; \mathrm{kg\cdot m/s} \). Final northward momentum: \( p_{2n} = 2 \times 5 \cos 60^\circ = 5 \; \mathrm{kg\cdot m/s} \). Change: \( \Delta p_n = 5 - 10 = -5 \; \mathrm{kg\cdot m/s} \).
    Answer: C

  7. Momentum conservation: \( 4 \times 6 + 6 \times 5 = (4 + 6)v_f \) ⇒ \( 54 = 10v_f \) ⇒ \( v_f = 5.4 \text{ m/s} \). Initial kinetic energy: \( K_i = \frac{1}{2}(4)(6^2) + \frac{1}{2}(6)(5^2) = 147 \text{ J} \). Final kinetic energy: \( K_f = \frac{1}{2}(10)(5.4^2) = 145.8 \text{ J} \). Loss: \( 145.8 - 147 = -1.2 \text{ J} \).
    Answer: A

  8. Momentum conservation (right positive): \( 0 = 1 \times (-9) + 3 \times v_B \) ⇒ \( 0 = -9 + 3v_B \) ⇒ \( v_B = 3 \text{ m/s} \) (positive ⇒ right).
    Answer: B

  9. Momentum is conserved in any collision (assuming no external forces). Kinetic energy is conserved only in elastic collisions.
    Answer: D

  10. Momentum conservation (right positive): \( m_1|v_1| + m_2(-|v_2|) = 0 \) ⇒ \( m_1|v_1| - m_2|v_2| = 0 \) ⇒ \( |v_2| = \frac{m_1|v_1|}{m_2} \).
    Answer: B