What is the Numerical Aperture of an Optical Fiber?

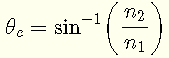
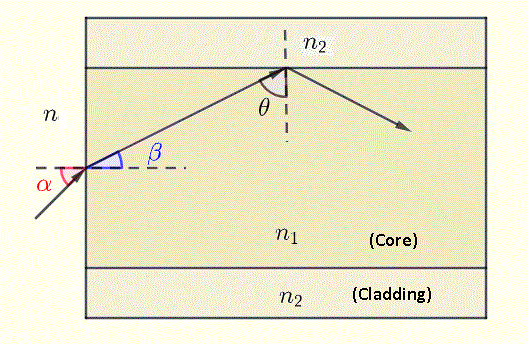
The optical fiber system shown below has a core of refractive index n₁ and a cladding of refractive index n₂ such that n₁ > n₂. For a light ray to be internally reflected at the core - cladding interface, the angle on incidence θ must be greater than the critical angle θ_c given by

Numerical Aperture of Optical Fiber Sytems Problems with Solutions

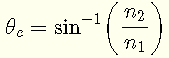
A numerical aperture of optical fibers calculator is included in this site and may be used to check the calculations in the following problems.

Problem 1

let n = 1, n₁ = 1.46 and n₂ = 1.45 in the diagram of the optical fiber system above. Find
a) the critical angle θ_c at the core - cladding interface.
b) the numerical aperture N.A. of the optical fiber
c) the angle of acceptance α_max of the the optical fiber system.
Solution to Problem 1
a) θ_c = sin^-1 (n₂ / n₁) = sin^-1 (1.45 / 1.46) = 83.29 °
b) N.A. = √(n²₁ - n²₂) = √(1.46² - 1.45²) = 0.17
c) α_max = sin^-1√(1.46² - 1.45²) = 9.82 °

Problem 2

We use the same values for n , n₁ and n₂ in the diagram of the optical fiber system above as those used in problem 1. Let the angle of incidence of a light ray on the outside - core interface be α = 5°. Find
a) angle of refraction β at the outside - core interface.
b) angle θ
c) and explain why this light ray will be reflected at the core - cladding interface and hence guided along the fiber.
Solution to Problem 2
a) Angle β is found using Snell's law at the outside - core interface as follows
n sin(α) = n₁ sin(β)
Substitute the given parameters from problem 1 to obtain
β = sin^-1 ( sin(5°) / n₁) = 3.42 °
b) Angle θ is complementary to angle β hence
θ = 90 - 3.42 = 86.58 °
c) The angle of incidence θ = 86.58 ° at the core - cladding interface is larger that the critical angle θ_c = 83.29 ° calculated in problem 1 above and will therefore be totally reflected at this interface and hence guided along the fiber.
Of course we could have answered this question by stating that since angle α = 5° is smaller to α_max = 9.82 ° calculated in problem 1, the given light ray will be reflected at the core - cladding interface, but the idea behind this problem is to gain better understanding of the concept of numerical aperture and angle of acceptance of an optical fiber systems using numerical values and calculations at each interface.

Problem 3

let n = 1 and n₁ = 1.48 in the diagram of the optical fiber system above. Find n₂ such that light rays incident at an angle α greater than 12 ° are not reflected at the core - cladding and therefore not guided along the optical fiber system.
Solution to Problem 3
In this problem, we are given α_max = 12 ° given by the formula
α_max = sin^-1(√(n₁² - n₂²)/ n)
The above is equivalent to
sin(α_max) = √(n₁² - n₂²)/ n
Substitute α_max, n and n₁ by the given values and calculate n₂
n₂² = n₁² - sin²(α_max)
n₂ = √(1.48² - sin²(12°)) = 1.465

Problem 4

let n = 1 in the diagram of the optical fiber system above. Find n₁ and n₂ such that the acceptance α_max = 10° and the critical angle at the core - cladding interface θ_c = 82 ° .
Solution to Problem 4
In this problem, we are given α_max and θ_c whose formulas are given by
\( \alpha_{max} = \sin^{-1} \left (\dfrac{1}{n} \sqrt{n_1^2-n_2^2} \right) \) and \(\theta_c = \sin^{-1} \left(\dfrac{n_2}{n_1} \right) \)
Take the sine of both sides in the formula of \( \alpha_{max} \)
\( \sin \left(\alpha_{max}\right) = \sin \left(\sin^{-1} \left (\dfrac{1}{n} \sqrt{n_1^2-n_2^2} \right) \right) \)
Simplify using the identity \( \sin (\sin^{-1} (x)) = x \)
\( \sin \left(\alpha_{max}\right) = \dfrac{1}{n} \sqrt{n_1^2-n_2^2} \)
square both sides to obtain
\(\sin^2\alpha_{max} = \left (\dfrac {n_1^2-n_2^2} {n^2} \right) \)
Take the sine of both sides in \(\theta_c = \sin^{-1} \left(\dfrac{n_2}{n_1} \right) \) and simplify to obtain
\(\sin \theta_c = \left(\dfrac{n_2}{n_1} \right) \)
Substitute the known values to obtain the equations
\(n_1^2-n_2^2 = n^2 \sin^2 \alpha_{max} \quad\quad (equation 1) \)
\(\dfrac{n_2}{n_1} = \sin \theta_c \quad\quad (equation (2) \)
Equation (2) gives
\(n_2 = n_1 \sin \theta_c \)
Substitute the above in equation (1) and solve for n₁ and n₂
\(n_1^2- (n_1 \sin \theta_c )^2 = n^2 \sin^2 \alpha_{max} \)
Rewrite the above as
\(n_1^2(1 - \sin^2 (\theta_c)) = n^2 \sin^2 \alpha_{max} \)
Solve for \(n_1^2 \)
\(n_1^2 = \dfrac{\sin^2 \alpha_{max} }{1 - \sin^2 \theta_c} = n^2 \dfrac{\sin^2 \alpha_{max}}{ \cos^2 \theta_c } \)
Take the square root of both sides in the above
\(n_1 = \dfrac{n\sin \alpha_{max} }{ \cos (\theta_c)} \)
Use equation 2 to find
\(n_2 = n_1 \sin \theta_c = \dfrac{n \sin(\alpha_{max})}{ \cos \theta_c} \sin \theta_c = n \sin \alpha_{max} \tan \theta_c \)
Substitute n , θ_c and α_max by their values to obtain numerical values for n₁ and n₂
\(n_1 = \dfrac{\sin 10^{\circ} }{ \cos 82^{\circ}} = 1.2477 \)
and
\(n_2 = \tan 82^{\circ} \sin 10^{\circ} = 1.2355 \)

More References and Links

Optical Fibers.
numerical aperture of optical fibers calculator
Total Internal Reflection of Light Rays at an Interface.
Refraction of Light Rays, Examples and Solutions.