Optical Lenses: Principles and Applications

Refraction of Light Rays in Different Situations

Understanding refraction is essential for studying convex and concave lenses. We examine the angle of deviation when light passes from a medium with refractive index $n_1$ to one with $n_2$.

Case 1: $n_1 < n_2$

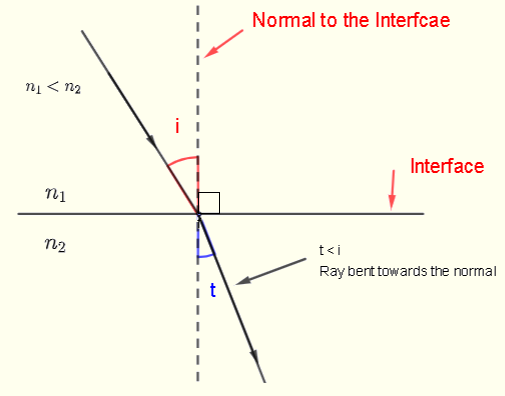
$Refraction towards the normal$

Snell's Law states:

\[n_1 \sin(i) = n_2 \sin(t)\]

Since $n_1/n_2 < 1$, we have:

\[\sin(t) = \frac{n_1}{n_2} \sin(i) < \sin(i) \quad \Rightarrow \quad t < i\]

The refracted ray bends toward the normal when entering a more optically dense medium.

Case 2: $n_1 > n_2$

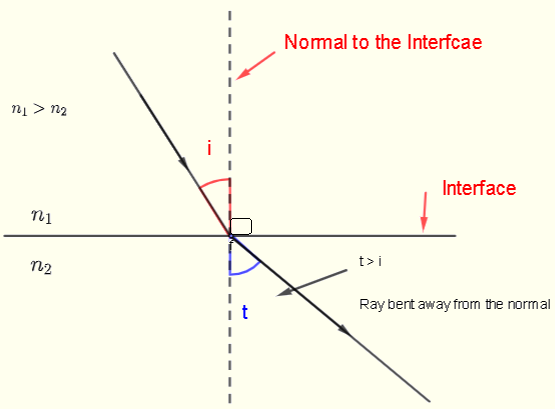
$Refraction away from the normal$

From Snell's Law with $n_1/n_2 > 1$:

\[\sin(t) = \frac{n_1}{n_2} \sin(i) > \sin(i) \quad \Rightarrow \quad t > i\]

The refracted ray bends away from the normal when entering a less dense medium.

Case 3: Normal Incidence ($i = 0$)

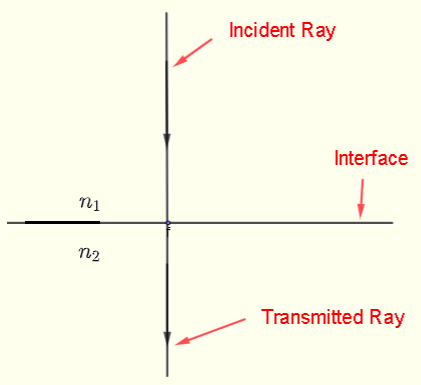
The ray transmits without deviation.

Example 1

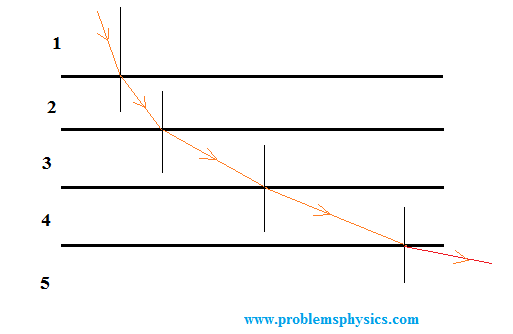
$Refraction through multiple media$

A light ray passes through five media with increasing refraction angles.

a) Which medium has the lowest refractive index?

b) Which medium has the lowest speed of light?

Solution

a) Increasing refraction angles indicate decreasing refractive indices. Medium 5 has the lowest $n$.

b) The speed in a medium is $v = c/n$. Medium 1 has the highest $n$, thus the lowest $v$.

Converging Lenses Principles

$Refraction causing convergence$

A triangular glass piece refracts incident rays downward. At side AB, refraction is toward the normal (air→glass). At side BC, refraction is away from the normal (glass→air). The net effect bends rays toward the horizontal axis.

A converging (convex) lens is shaped so parallel rays converge at a focal point.

Diverging Lenses Principles

$Refraction causing divergence$

Here, refraction at AB bends the ray away from the horizontal. Refraction at BC further bends it upward. The net effect diverges rays from the axis.

A diverging (concave) lens causes parallel rays to spread apart.

Optical Lenses Applications

Human eyes
Astronomical telescopes
Binoculars
Magnifying glasses
Microscopes
Eyeglasses and contact lenses

References

Snell's Law
Principles of Optics – Max Born, Emil Wolf (Cambridge University Press)
Optics and Optical Instruments – B.K. Johnson
Introduction to Lens Design – José Sasián