Three online calculators to calculate all the currents and voltages in three different dc circuit are presented. Practice solving dc circuits manually and check answers using these calculators.
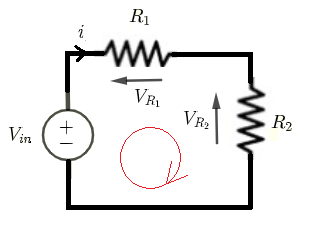Given \( V_{in} \) , \( R_1 \) and \( R_2 \), let us find formulas for the currents through and the voltages across all resistors.
Using Kirchhoff's laws of voltages to write the equations:
\( V_{in} = R_1 i + R_2 i \) (I)
Solve for \( i \)
\( i = \dfrac{V_{in}}{R_1 + R_2} \)
Use Ohm's law to find the voltages
\( V_{R_1} = i R_{1} = \dfrac{ R_{1} V_{in}}{R_1 + R_2} \)
\( V_{R_2} = i R_{2} = \dfrac{ R_{2} V_{in}}{R_1 + R_2} \)
Enter the voltage source \( V_{in} \) in volts and the resistors \( R_1\) and \( R_4 \) in \( \Omega \) and press "Calculate". The calculator uses the above formulas to calculates all currents and voltages whose formulas were obtained above.
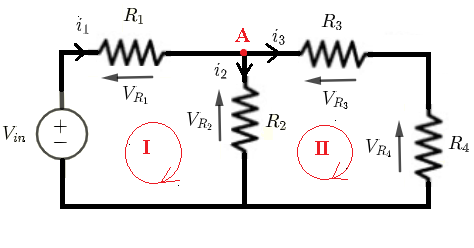Given \( V_{in} \) , \( R_1 \), \( R_2 \), \( R_3 \) and \( R_4 \), let us find formulas for the currents through and the voltages across all resistors.
Using Kirchhoff's laws of voltages to write the equations:
Loop (I): \( V_{in} = R_1 i_1 + R_2 i_2 \) (I)
Loop (II): \( - R_2 i_2 + R_3 i_3 + R_4 i_3 = 0 \) (II)
Using Kirchhoff's laws of currents to write the equation:
Node (A): \( i_1 = i_2 + i_3 \) (III)
Substitute \( i_1 \) by \( i_2 + i_3 \) in equations (I) and rearrange equations (I) and (II) to have a system in two equations and two unknowns \( i_2 \) and \( i_3 \)
\( (R_1 + R_2) i_2 + R_1 i_3 = V_{in} \)
\( - R_2 i_2 + (R_3 + R_4) i_3 = 0 \)
Use any method to solve the above system of equations to obtain
\( i_2 = \dfrac{R_3 + R_4}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( i_3 = \dfrac{R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
Use equation (III) to find \( i_1 \)
\( i_1 = i_2+i_3 = \dfrac{R_2+R_3 + R_4}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
The voltages across the resistors are given by Ohm's law as follows:
\( V_{R_1} = R_1 i_1 = \dfrac{R_1(R_2 + R_3 + R_4)}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_2} = R_2 i_2 = \dfrac{R_2(R_3 + R_4)}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_3} = R_3 i_3 = \dfrac{R_3 R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_4} = R_4 i_3 = \dfrac{R_4 R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
Enter the voltage source \( V_{in} \) in volts and the resistors \( R_1, R_2, R_3 \) and \( R_4 \) in \( \Omega \) and press "Calculate". The calculator uses the above formulas to calculates all currents and voltages whose formulas were obtained above.
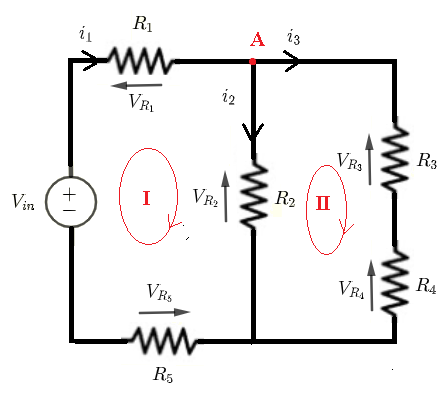Given \( V_{in} \) , \( R_1 \), \( R_2 \), \( R_3 \) , \( R_4 \) and \( R_5 \), let us find formulas for the currents through and the voltages across all resistors.
Using Kirchhoff's laws of voltages to write the equations:
Loop (I): \( V_{in} = R_1 i_1 + R_2 i_2 + R_5 i_1 \) (I)
Loop (II): \( - R_2 i_2 + R_3 i_3 + R_4 i_3 = 0 \) (II)
Using Kirchhoff's laws of currents to write the equation:
Node (A): \( i_1 = i_2 + i_3 \)
Equation (I) obtained from Kirchhoff's laws for circuits 2 is given by
\( V_{in} = R_1 i_1 + R_2 i_2 \)
Equation (I) obtained from Kirchhoff's laws for circuits 3 above is given by
\( V_{in} = R_1 i_1 + R_2 i_2 + R_5 i_1 = (R_1 + R_5) i_1 + R_2 i_2 \)
The only difference is that the coefficient of \( i_1 \) is \( R_1 + R_5 \) in circuit 3 and \( R_1 \) in circuit 2. We therefore do need to solve the system of the three equations from start, but we just replace
\( R_1 \) in the solutions for circuit 2 by \( R_1 + R_5 \) to obtain the solutions for circuit 3 which are given by
\( i_1 = \dfrac{R_2+R_3 + R_4}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( i_2 = \dfrac{R_3 + R_4}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( i_3 = \dfrac{R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
The voltages across the resistors are given by:
\( V_{R_1} = R_1 i_1 = \dfrac{R_1(R_2+R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_2} = R_2 i_2 = \dfrac{R_2(R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_3} = R_3 i_3 = \dfrac{R_3 R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_4} = R_4 i_3 = \dfrac{R_4 R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_4} = R_5 i_1 = \dfrac{R_5(R_2+R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
Enter the voltage source \( V_{in} \) in volts and the resistors \( R_1, R_2, R_3, R_4\) and \( R_5 \) in \( \Omega \) and press "Calculate". The calculator uses the above formulas to calculates all currents and voltages whose formulas were obtained above.
