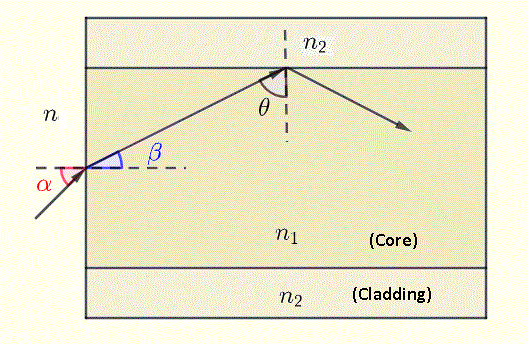
The numerical aperture of an optical fiber system as the one shown in the diagram below, has been defined and all important formulas found.
For a core of refractive index n1 and a cladding of refractive index n2 such that n1 > n2,
a light ray incident from outside the core at an angle α will be internally reflected at the core - cladding interface, if α is smaller that αmax
given by the formula
\alpha_{max} = \sin^{-1} \left (\dfrac{1}{n} \sqrt{n_1^2-n_2^2} \right)
Other formulas related to the critical angle at the core - cladding interface θ c and the numerical aperture N.A. are given by
\theta_c = \sin^{-1} \left(\dfrac{n_2}{n_1} \right)
N.A = \sqrt{n_1^2-n_2^2}
The angle of refraction β at the outside - core interface and angle of incidence α are related by
n \sin\alpha = n_1 \sin\beta
and the angle of incidence at the core - cladding interface θ and angle β are complementary.
\theta = 90^{\circ} - \beta
Two calculators that uses the above formulas are presented below.
1 - Calculate Numerical Aperture and αmax
Enter the refractive index of the outside n, the refractive index of the core n 1 , the refractive index of the cladding n 2 and the angle of incidence α of the ray coming from the left outside the fiber then press "Calculate".The outputs are: the angle of refraction β at the outside - core interface, the angle of incidence θ at the core - cladding Interface, the critical angle θ c at the Core - cladding interface, the numerical aperture N.A. and the maximum angle α maxc for which total internal refraction inside the fiber occurs which also called the angle of acceptance.
2 - Calculate Refractive Indices Given Critical θc Angle and αmax
Enter the refractive index of the outside n, the critical angle θ c at the core - cladding interface, the angle of acceptance α max then press "Calculate".The outputs are the refractive indices of the core n 1 and of the cladding n 2 .
More References and Links
Numerical Aperture of Optical Fibers .Optical Fibers .
Total Internal Reflection of Light Rays at an Interface .
