An online resultant force calculator is presented.
Resultant Force
The resultant force due to several forces \( \vec {F}_1, \vec {F}_2, ... \) acting on an object is the force \( \vec {R}f \) that has the same physical effects as the different forces acting on that object.
Mathematically, the resultant \( \vec {R}f \) force is given by the vector addition of all forces acting on the object.
\[ \vec {R}f = \vec {F}_1 + \vec {F}_2 + .... \]
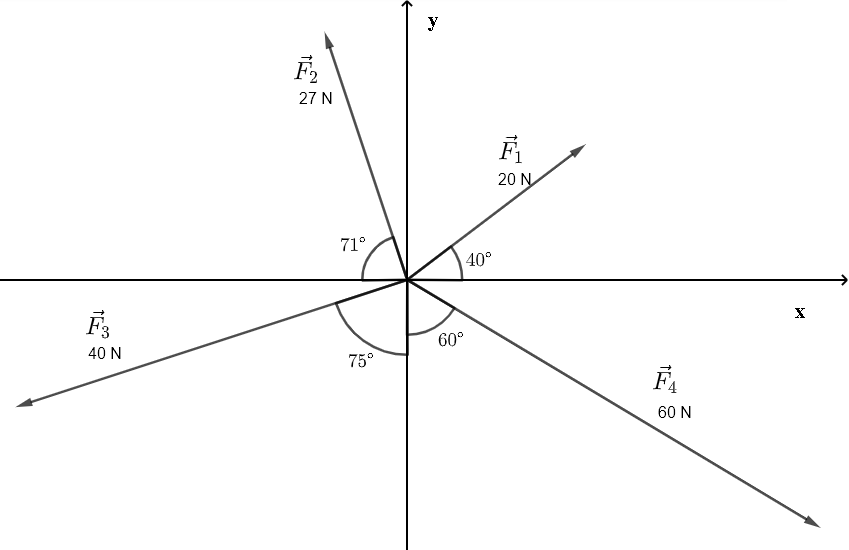
Given the magnitude and direction of each force, the calculator presented below, calculates the components of each given force, then add the \( x \) components of the forces \( \vec {F}_1, \vec {F}_2, ... \) to obtain the \( x \) component of \( R_{fx} \) and then add the \( y \) components of the forces \( \vec {F}_1, \vec {F}_2, ... \) to obtain the \( y \) components of \( R_{fy} \),
The magnitude \( |\vec {R}f| \) and direction \( \theta \) of the resultant force \( \vec {R}f \) are given by
\[ |\vec {R}f| = \sqrt { ( R_{fx} )^2 + ( R_{fy} )^2} \]
\[ \theta = \tan^{-1} \left({\frac{R_{fy}}{R_{fx}}}\right) \] with \( \theta \) is in the range \( [0 , 2\pi) \) taking into account the quadrant where the components of the resultant \( \vec {R}f \) are.
Use of the Resultant Force Calculator
1 - Enter the magnitude \( |F_i| \) and the direction of each force.
Important
A) The direction is the angle measured from the positive side of the x axis and is in degrees.
B) The magnitudes and directions of the four forces \( \vec {F}_1, \vec {F}_2, \vec {F}_3, \vec {F}_4, \) in the diagram above are used as the default values when you start this page. The directions given by different angles have all been converted to angles from the positive x axis to the force represented by a vector in the diagram above.
2 - Click "Calculate" to obtain \( R_{fx} \) and \( R_{fy} \) which are the x and y components of the resultant \( \vec {R}f \), its magnitude and its direction \( \theta \) defined above.