AP Physics Practice Questions: Dynamics

AP Physics multiple choice questions on dynamics, forces, and Newton's laws. Each question includes detailed solutions at the bottom of the page.

1. A 5.0 kg block is pulled along a horizontal frictionless surface by a string that makes an angle of 30° with the horizontal. If the tension in the string is 20 N, what is the acceleration of the block?

   A) 1.73 m/s²
   B) 2.00 m/s²
   C) 3.46 m/s²
   D) 4.00 m/s²
   E) 5.77 m/s²

2. Two blocks are connected by a massless string over a frictionless pulley as shown. Block A has mass 4.0 kg and block B has mass 6.0 kg. What is the acceleration of the system?

   

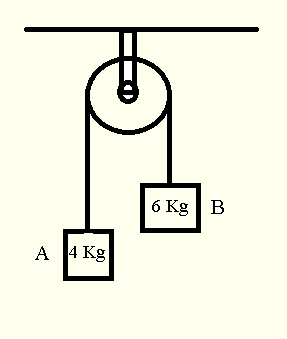
   A) 1.96 m/s²
   B) 2.94 m/s²
   C) 3.92 m/s²
   D) 4.90 m/s²
   E) 5.88 m/s²

3. A 2.0 kg block slides down a 30° incline with constant velocity. What is the coefficient of kinetic friction between the block and the incline?

   A) 0.29
   B) 0.50
   C) 0.58
   D) 0.71
   E) 0.87

4. A car of mass 1200 kg travels around a flat curve of radius 50 m at 15 m/s. What minimum coefficient of static friction is needed to prevent skidding?

   A) 0.23
   B) 0.35
   C) 0.46
   D) 0.58
   E) 0.69

5. A 10 kg block rests on a horizontal surface with μₛ = 0.5 and μₖ = 0.3. A force of 40 N is applied at 40° above the horizontal. What is the acceleration of the block?

   A) 0 m/s²
   B) 1.23 m/s²
   C) 1.64 m/s²
   D) 2.05 m/s²
   E) 2.46 m/s²

Solutions

1. C) 3.46 m/s²
   Only the horizontal component of tension accelerates the block:
   \( F_x = T\cos30° = 20 \times 0.866 = 17.32 \, \text{N} \)
   \( a = \dfrac{F_x}{m} = \dfrac{17.32}{5.0} = 3.46 \, \text{m/s}^2 \)

2. A) 1.96 m/s²
   For block B (6 kg, downward positive): \( m_B g - T = m_B a \)
   For block A (4 kg, upward positive): \( T - m_A g = m_A a \)
   Adding equations: \( m_B g - m_A g = (m_A + m_B) a \)
   \( a = \dfrac{(6.0 - 4.0) \times 9.8}{4.0 + 6.0} = \dfrac{19.6}{10} = 1.96 \, \text{m/s}^2 \)

3. C) 0.58
   Constant velocity ⇒ net force = 0
   Parallel to incline: \( mg\sin\theta - f_k = 0 \)
   Perpendicular to incline: \( N = mg\cos\theta \)
   \( f_k = \mu_k N = \mu_k mg\cos\theta \)
   \( mg\sin\theta = \mu_k mg\cos\theta \)
   \( \mu_k = \tan\theta = \tan30° = 0.577 \approx 0.58 \)

4. C) 0.46
   Friction provides centripetal force: \( f_s = \dfrac{mv^2}{r} \)
   Maximum static friction: \( f_{s,\max} = \mu_s N = \mu_s mg \)
   \( \mu_s mg = \dfrac{mv^2}{r} \)
   \( \mu_s = \dfrac{v^2}{rg} = \dfrac{15^2}{50 \times 9.8} = \dfrac{225}{490} = 0.459 \approx 0.46 \)

5. A) 0 m/s²
   Vertical forces: \( N = mg - F\sin40° = 98.1 - 40 \times 0.643 = 98.1 - 25.72 = 72.38 \, \text{N} \)
   Maximum static friction: \( f_{s,\max} = \mu_s N = 0.5 \times 72.38 = 36.19 \, \text{N} \)
   Horizontal applied force: \( F_x = F\cos40° = 40 \times 0.766 = 30.64 \, \text{N} \)
   Since \( F_x < f_{s,\max} \), Static friction is sufficient to keep the block at rest and the block does not move, so its acceleration is zero.