
Hooke's Law is a fundamental principle in physics that describes the behavior of elastic materials when subjected to external forces. Understanding this law is essential for studying mechanical systems, structural engineering, and material science.
In the diagram below, we examine a block attached to a spring in three different configurations:

In configuration (A), the spring is at its equilibrium position with no external force applied. In position (B), an applied force \( F \) compresses the spring by displacement \( \Delta x \). In position (C), the same magnitude of force \( F \) stretches the spring by displacement \( \Delta x \).
Hooke's Law mathematically expresses the relationship between the applied force and spring displacement:
Where:
According to Newton's Third Law, the spring exerts an equal and opposite restoring force \( -F \) when stretched or compressed.
What magnitude of force is required to stretch a 20 cm-long spring (spring constant \( k = 100 \, \text{N/m} \)) to a length of 21 cm?
SolutionThe spring elongation is calculated as:
\[ \Delta x = 21 \, \text{cm} - 20 \, \text{cm} = 1 \, \text{cm} = 0.01 \, \text{m} \]Applying Hooke's Law:
\[ |F| = k |\Delta x| = 100 \, \text{N/m} \times 0.01 \, \text{m} = 1 \, \text{N} \]A force of 1 N is required to produce this elongation.
A spring requires 3 N of force to compress it from 40 cm to 35 cm. What is its spring constant?
SolutionThe compression distance is:
\[ \Delta x = 40 \, \text{cm} - 35 \, \text{cm} = 5 \, \text{cm} = 0.05 \, \text{m} \]Using Hooke's Law:
\[ k = \frac{|F|}{|\Delta x|} = \frac{3 \, \text{N}}{0.05 \, \text{m}} = 60 \, \text{N/m} \]The spring constant is 60 N/m, indicating a relatively stiff spring.
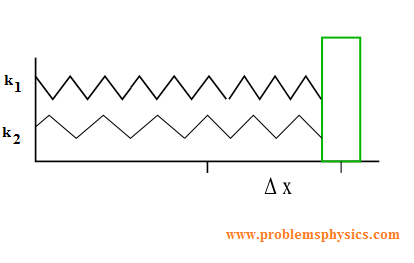
When springs are arranged in parallel, they share the applied load. The combined spring constant for parallel springs is the sum of individual constants:
This arrangement results in a stiffer composite spring system than any individual spring.
Two springs with constants \( k_1 = 100 \, \text{N/m} \) and \( k_2 = 200 \, \text{N/m} \) are connected in parallel. What force is required to stretch this system by 6 cm?
SolutionThe equivalent spring constant for parallel arrangement:
\[ k_{\text{eq}} = k_1 + k_2 = 100 \, \text{N/m} + 200 \, \text{N/m} = 300 \, \text{N/m} \]Applying Hooke's Law with \( \Delta x = 0.06 \, \text{m} \):
\[ |F| = k_{\text{eq}} |\Delta x| = 300 \, \text{N/m} \times 0.06 \, \text{m} = 18 \, \text{N} \]The parallel configuration requires 18 N, significantly more than either spring alone would require.
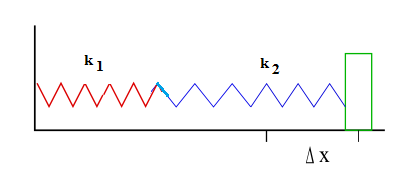
In series arrangements, springs experience the same force but different displacements. The reciprocal of the combined spring constant equals the sum of reciprocals of individual constants:
Series combinations produce a less stiff composite spring than any individual component.
The same springs (\( k_1 = 100 \, \text{N/m} \), \( k_2 = 200 \, \text{N/m} \)) are now connected in series. What force is needed to stretch this combination by 6 cm?
SolutionCalculate the equivalent spring constant:
\[ \frac{1}{k_{\text{eq}}} = \frac{1}{100} + \frac{1}{200} = \frac{3}{200} \] \[ k_{\text{eq}} = \frac{200}{3} \approx 66.67 \, \text{N/m} \]Applying Hooke's Law:
\[ |F| = k_{\text{eq}} |\Delta x| \approx 66.67 \, \text{N/m} \times 0.06 \, \text{m} \approx 4.0 \, \text{N} \]The series arrangement requires only 4.0 N, making it more easily stretched than the parallel configuration.
When a spring is deformed, work is done against the restoring force. This work is stored as elastic potential energy, given by:
Where \( U \) represents the potential energy in joules (J). This energy is recoverable when the spring returns to its equilibrium position.
How much work is required to compress a spring ( \( k = 150 \, \text{N/m} \) ) from 15 cm to 10 cm?
SolutionThe compression distance:
\[ \Delta x = 10 \, \text{cm} - 15 \, \text{cm} = -5 \, \text{cm} = -0.05 \, \text{m} \]The work done equals the stored potential energy:
\[ W = U = \frac{1}{2} k (\Delta x)^2 = \frac{1}{2} \times 150 \, \text{N/m} \times (-0.05 \, \text{m})^2 = 0.1875 \, \text{J} \]Thus, 0.1875 joules of energy are stored in the compressed spring.