Displacement and Distance: Tutorials with Examples

Examples with explanations on displacement and distance of objects moving along straight lines. More problems and their solution can be found in this site.

The distance is a scalar quantity (magnitude) that describes the length of the total path covered by a moving object.

The displacement is a vector quantity (magnitude and direction) that describes the difference between the final and initial positions of a moving object. It is the shortest distance moved in a certain direction. Both distance and displacement are measured in unit of lengths. (centimeters, meters, kilometers,...)

Example 1: An object moves from A to D along the red path as shown below.

a) Find the total distance covered by the object

b) Find the displacement of the object

displacement and distance - Example 1
Solution:

a) Using the given scale (1km per division); the total distance d is given by

d = AB + BC + CD = 2 + 5 + 2 = 9 km

b) The final and initial and positions of the moving object are used to find the displacement. The distance from A (initial position) to D (final position) is equal to AD = 5 km.

The displacement is the vector AD whose magnitude if 5 km and its direction is to the east.

Example 2: An object moves, along a line, from point A to B to C and then back to B again as shown in the figure below.

a) Find the distance covered by the moving object.

b) Find the magnitude of the displacement of the object.

displacement and distance - Example 2
Solution:

a) The total distance d covered by the object is

d = AB + BC + CB = 5 km + 4 km + 4 km = 13 km

b) The magnitude of the displacement is equal to the distance from A (initial position) to B (final position) which is equal to 5 km.

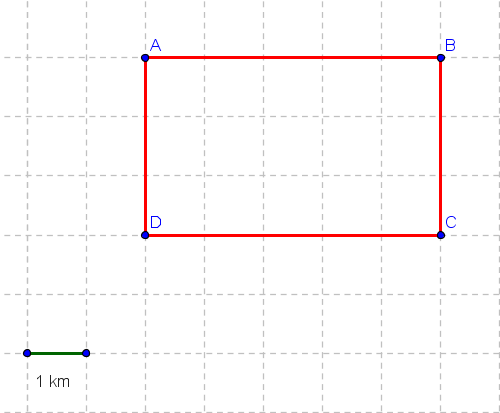
Example 3: An object moves from point A to B to C to D and then back to A along the rectangle shown in the figure below.

a) Find the total distance covered by the moving object.

b) Find the displacement of the object.

displacement and distance - Example 3
Solution:

a) The total distance d is equal to the perimeter of the rectangle. Using the given scale,

d = 2 AB + 2 BC = 10 + 6 = 16 km

b) Since the moving object starts at point A and finish at A, there is no change in the position of the object and therefore the displacement is equal to zero.

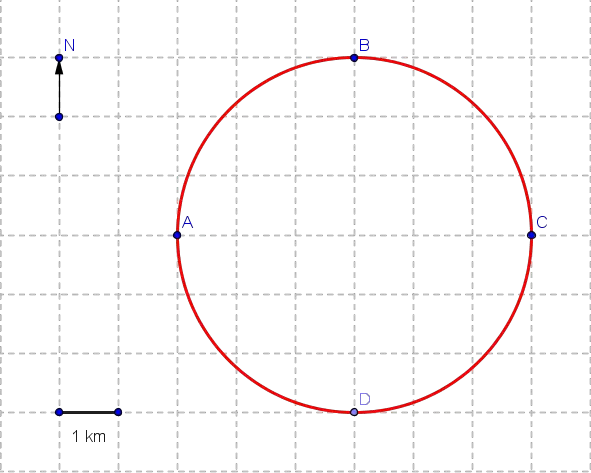
Example 4: An object moves from point A to B to C along the circle as shown in the figure below.

a) Find the total distance covered by the moving object.

b) Find the displacement of the object.

displacement and distance - Example 4
Solution:

a) The total distance d is equal to half the circumference of the circle and given by

d = (1/2)(2 * Pi * 3) = 3 Pi km

b) The magnitude of the displacement D is equal to the diameter AC of the circle and is given by

D = 2 * 3 = 6 km with direction to the East

Example 5: An object moves from point A to point B along the circle as shown in the figure below.

a) Find the total distance covered by the moving object.

b) Find the magnitude of the displacement of the object.

displacement and distance - Example 5
Solution:

a) The total distance d is equal to the quarter the circumference of the circle and given by

d = (1/4)(2 * Pi * 3) = 1.5 Pi km

b) The magnitude of the displacement D is equal to the hypotenuse AB of the right angle ABO as shown below

displacement and distance - Solution to Example 5
Use Pythagora's theorem to find AB as follows

AB2 = 32 + 32 = 18

D = AB = 3√2 km

privacy policy