Velocity and Speed: Tutorials with Examples

Examples with explanations on the concepts of average speed and average velocity of moving object. More problems and their solutions can be found in this website.

The average speed is a scalar quantity (magnitude) that describes the rate of change (with the time) of the distance of a moving object.

average speed =  
distance
time

The average velocity is a vector quantity (magnitude and direction) that describes the rate of change (with the time) of the position of a moving object.


average velocity =  
change in position
time
=  
displacement
time

Example 1: An object moves from A to D along the red path as shown below in 41 minutes and 40 seconds.

a) Find the average speed of the object in m/s

b) Find the average velocity of the object in m/s

displacement and distance - Example 1
Solution:

a) Using the given scale (1km per division); the total distance d is given by

d = AB + BC + CD = 2 + 5 + 2 = 9 km

average speed =  
distance
time
=
9 km
41 mn + 40 s
=  
9000 m
(41*60 + 40) s
=  
9000 m
2500 s
 = 3.6 m/s


b) The final and initial and positions of the moving object are used to find the displacement. The distance from A (initial position) to D (final position) is equal to AD = 5 km. The displacement is the vector AD whose magnitude if 5 km and its direction is to the east.


average velocity =  
displacement
time
=  
5 km
41 mn + 40 s
=  
5000 m
2500 s
 = 2.5 m/s



The average velocity is a vector whose magnitude is 2.5 m/s and its direction is to the east.

Example 2: An object moves, along a line, from point A to B to C and then back to B again as shown in the figure below in half an hour.

a) Find the average speed of the moving object in km/h.

b) Find the magnitude of the average velocity of the object in km/h.

displacement and distance - Example 2

Solution:

a) The total distance d covered by the object is

d = AB + BC + CB = 5 km + 4 km + 4 km = 13 km

average speed =  
distance
time
=
13 km
0.5 hour
 = 26 km/h

b) The magnitude of the displacement is equal to the distance from A (initial position) to B (final position) which is equal to 5 km.


average velocity =  
displacement
time
=  
5 km
0.5 hour
 = 10 km/h

Example 3: An fast object moves from point A to B to C to D and then back to A along the rectangle shown in the figure below in 5 seconds.

a) Find the average speed of the moving object in m/s.

b) Find the velocity of the object in m/s.

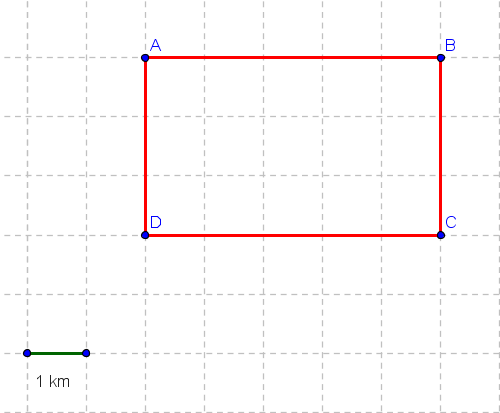
displacement and distance - Example 3
Solution:

a) The total distance d is equal to the perimeter of the rectangle. Using the given scale,

d = 2 AB + 2 BC = 10 + 6 = 16 km

average speed =  
distance
time
=
16 km
5 seconds
=
16000 m
5 seconds
 = 3200 m/s

b) Since the moving object starts at point A and finish at A, there is no change in the position of the object and therefore the displacement is equal to zero.


average velocity =  
displacement
time
=  
0
5 second
 = 0

Example 4: A person walks, for two hours, from point A to B to C along a circular field as shown in the figure below.

a) Find the average speed of the person in km/h.

b) Find the velocity of the person.

displacement and distance - Example 4
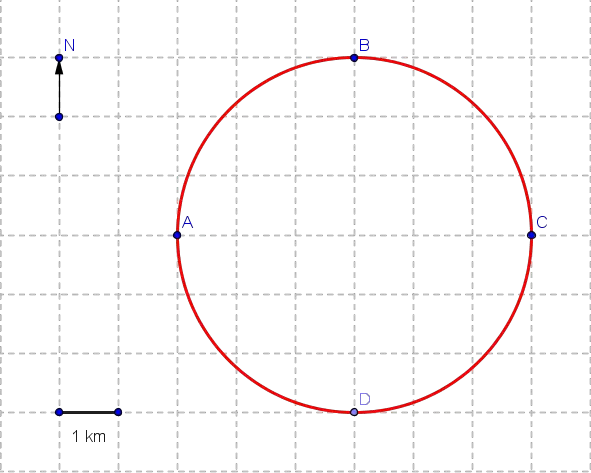
Solution:

a) The total distance d is equal to half the circumference of the circle and given by

d = (1/2)(2 * Pi * 3) = 3 Pi

average speed =  
distance
time
=
3 Pi km
2 hours
 = 1.5 Pi km/h = 4.7 km/h



b) The magnitude of the displacement D is equal to the diameter AC of the circle and is given by

D = 2 * 3 = 6 Km with direction to the East


average velocity =  
displacement
time
=  
6 km
2 hours
 = 3 km/h

Example 5: A person walks for one hour and 12 minutes, from point A to point B, along a circular field as shown in the figure.

a) Find the average speed of the person in km/h.

b) Find the magnitude of the displacement of the person in km/h.

displacement and distance - Example 5
Solution:

a) The total distance d is equal to the quarter the circumference of the circle and given by

d = (1/4)(2 * Pi * 3) = 1.5 Pi

average speed =  
distance
time
=
1.5 Pi km
1 hour + 12 minutes
=
1.5 Pi km
1 hour + 12/60 hour
=
1.5 Pi km
1.2 hour

= 1.25 Pi km/h = 3.9 km/h



b) The magnitude of the displacement D is equal to the hypotenuse AB of the right angle ABO as shown below

displacement and distance - Solution to Example 5
Use Pythagora's theorem to find AB as follows

AB2 = 32 + 32 = 18

D = AB = 3√2 km


average velocity =  
displacement
time
=  
3√2 km
1 hour + 12 minutes
=  
3√2 km
1.2 hours

= 2.5√2 km/h = 3.5 km/h