Electrostatic charges and forces problems are presented along with detailed solutions.
Problems
Problem 1:
What is the net force and its direction that the charges at the vertices A and C of the right triangle ABC exert on the charge in vertex B?
Solution to Problem 1:
Let F AB be the force of repulsion exerted by the charge at A on the charge at B and F CB be the force exerted by the charge at point C on the charge at point B. The diagram below shows the direction of these two forces.
|F AB | = k (7 × 10 -6 )((2× 10 -6 ) / (4 × 10 -2 ) 2 = 14 × 10 -12 k / (16 × 10 -4 ) = 0.875 k × 10 -8 N
|F CB | = k (2× 10 -6 )(2× 10 -6 ) / (2 × 10 -2 ) 2 = k × 10 -8 N
We now use the Pythagorean theorem to find the magnitude of the resultant force F = F AB + F CB (a vector sum)
|F| = √(|F AB | 2 + |F CB | 2 ) = k × 10 -8 √( 0.875 2 + 1 2 ) = 9.00 × 10 9 × 10 -8 √( 0.875 2 + 1 2 ) = 1.20 × 10 2 N
θ = arctan(|F CB |/ |F AB | ) = arctan( k × 10 -8 / 0.875 k × 10 -8 ) = 48.8°
Problem 2:
A positive charge q exerts a force of magnitude - 0.20 N on another charge - 2q. Find the magnitude of each charge if the distance separating them is equal to 50 cm.
Solution to Problem 2:
The force that q exerts on 2q is given by Coulomb's law:
F = k (q) ( - 2q) / r2 ,
Given: r = 0.5 m , F = - 0.20 N ,
Use the formula of F above to write the equation
- 0.2 = - 2 q2 k / 0.52
k is Coulomb constant (k ≈ 9 × 109 )
Solve for q2
q2 = 0.2 × 0.52 / (2 k)
q = √ [ (0.2 × 0.52 / (2 × 9 × 109) ] = 1.66 × 10-6 C
The two charges are:
q = 1.66 × 10-6 C,
-2 q = -3.23 × 10-6 C
Problem 3:
Two identical objects, separated by a distance d, with charges equal in magnitude but of opposite signs, exert a force of attraction of - 2.5 N on each other. What force do these objects exert on each other if the distance between them becomes 2d?
Solution to Problem 3:
Let the two charges be q and -q. The magnitude of the force that q and -q, separated by a distance d, exert on each other is given by Coulomb's law:
F = k (q) (- q) / d2 = - k q2 / d2 = - 2.5 N
The magnitude of the force F2 that q and -q, separated by a distance 2 d, exert on each other is given by Coulomb's law:
F2 = k (q) (- q) / (2 d)2 = - k q2 / 4 d2 = F / 4 = - 2.5 / 4 = - 0.625 N
Problem 4:
A charge of q = - 4.0 × 10-6 is placed in an electric field and experiences a force of 5.5 N [E]
a) What is the magnitude and direction of the electric field at the point where charge q is located?
b) If charge q is removed, what is the magnitude and direction of the force exerted on a charge of - 2q at the same location as charge q?
Solution to Problem 4:
a) The force on a charge q due to an electric field E is given by
F = q E
The magnitude of E is given by
| E | = | F | / | q | = 5.5 / (4.0 × 10-6) = 1.375 × 106 N / C
Since charge q is negative F and E have opposite directions. E is 1.375 × 106 N / C [W]
b) The force on a charge -2q due to an electric field E is given by
F2 = -2 q E = -2(q E) = -2(5.5[E]) = -11 [E] or 11 N [W]
Problem 5:
Three charges are located at the vertices of a right isosceles triangle as shown below. What is the magnitude and direction of the resultant electric field at the midpoint M of AC?
Solution to Problem 5:
The magnitude of an electric field due to a charge q is given by.
E = k q / r 2
and it is directed away from charge q if q is positive and towards charge q if q is negative. Hence the diagram below shows the direction of the fields due to all three charges. The total field E is the vector sum of all three fields: E AM , E CM , and E BM
E = E AM + E CM + E BM (vector sum)
Because of the symmetry at point M, E AM , and E CM are equal in magnitudes and opposite directions. Hence
E AM + E CM = 0 (vector addition)
Hence
E = E BM
The magnitude of E BM is given by
E BM = k (2 × 10 -6 ) / BM 2
Note that
∠MBA = ∠MAB = 45° and MB = MA (lengths)
hence
MB = MA
Use the Pythagora's theorem to write
5 2 = MB 2 + MA 2
MB = 5/√2
MB 2 = 25/2 = 12.5 cm 2 = 12.5×10 -4 m 2
The magnitude of the field E BM at point M due to the charge at B is given by
E BM = k q / MB 2 = k (2 × 10 -6 ) / (12.5 × 10 -4) = 9.00 × 10 9 × 2 × 10 -6 / (12.5 × 10 -4 ) = 1.44 × 10 7 N/C
The magnitude of the total field E at M is equal to E BM , hence
E = E BM = 1.44 × 10 7 N/C
Problem 6:
What distance must separate two charges of + 5.6×10-4C and -6.3×10-4 C in order to have electric potential energy with a magnitude of 5.0 J in the system of the two charges?
Solution to Problem 6:
The magnitude of the electric potential energy Ep of a system of two charges q1 and q2 separated by a distance r is given by
Ep = k | q1 | | q2 | / r
Solve for r.
r = k q1 q2 / Ep = 9.00×109×5.6×10-4×6.3×10-4 / 5.0 = 6.35×102 m
Problem 7:
The distance between two charges q1 = + 2 μC and q2 = + 6 μC is 15.0 cm. Calculate the distance from charge q1 to the points on the line segment joining the two charges where the electric field is zero.
Solution to Problem 7:
At a distance x from q1, the total electric field is the vector sum of the electric E1 from due to q1 and directed to the right and the electric field E2 due to q2 and directed to the left. The vector sum is equal to zero if the magnitudes of the two fields E1 and E2 are equal since they have opposite directions.
The magnitudes of the two fields E 1 and E 2 are given by
E 1 = k q1 / x 2
E 2 = k q2 / (15 - x) 2
E 1 = E 2 gives the equation
k q1 / x 2 = k q2 / (15 - x) 2
Cross multiply and simplify to obtain
q1(15 - x) 2 = q2 x 2
Which may be written as
(15 - x) 2 / x 2 = q2 / q1 = 3
We now to solve for x the equation
(15 - x) / x = ~+mn~ √3
The above equation gives two solutions but only one is positive and is equal to
x = 15 / (1 + √3) ≈ 5.50 cm
Problem 8:
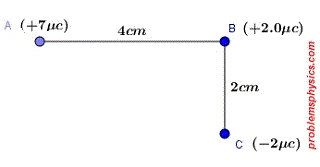
The distance AB between charges Q1 and Q2 shown below is 5.0 m. How much work must be done to move charge Q2 to a new location at point C so that the distance BC = 2.5 m?
Solution to Problem 8:
If W is the work to be done to move Q2 from a position where its potential energy is E p1 and kinetic energy 0 (from rest) to another position where its potential energy is E p2 and kinetic energy 0 (to rest), then by the conservation of energy, we have.
E p1 + W = E p2
which gives
W = E p2 - E p1
E p1 = k Q1 Q2 / AB , with AB = 5 m
E p2 = k Q1 Q2 / AC , with AC = 7.5 m
W = k Q1 Q2 (1/AB - 1/AC) = 9.00×10 9 ×5×10 -6 ×-3×10 -6 (1/7.5 - 1/5) = 9×10 -3 J
Problem 9:
Two parallel plates separated by a distance of 1 cm have a potential difference of 20 V between them. The plates are held in a horizontal position with the negative plate above the positive plate. An electron is released from rest in the upper plate.
a) What is the acceleration of the electron?
b)How long it takes to reach the lower plate?
c)What is the kinetic energy of the electron when it hits the lower plate?
Note: charge of electron q = -1.6×10-19C , mass of electron m = 9.11×10-31Kg
Solution to Problem 9:
a) Electric force F exerted on the electron is given by:
F = q E
with the electric field E between the plates given by:
E = ΔV / d = 20 v / 1 cm = 2000 v/m or N/C
F = -1.6×10 -19 C×2000 N/C = -3.2×10 -16 N
Note: the weight of the electron is given by: m g = 9.11×10 -31 ×9.8 = 8.93×10 -30 N
which is much smaller than the electric force acting on the electron and will therefore be neglected.
The acceleration due to the electric force is:
a = F / m = -3.2×10 -16 /9.11×10 -31 = - 3.51×10 14 m/s 2
b) Let v f and v i be the final (at the lower plate) and initial (from rest at the upper plate ) velocities of the electron. Hence using the formula
v f2 = v i2 + 2 a h
h is the distance between the plates.
v i = 0 (from rest)
v f2 = 2 a h = 2(- 3.51×10 14 m/s 2 )(-1×10 -2 m) (y axis upward)
v f = 2.64×10 6 m/s
With uniform acceleration a and initial velocity equal to zero, we have the velocity as a function of time given by
v = a t
If T is the time it takes the electron to move from the upper to the lower plates, then
v f = a T
which gives
T = v f / a = 2.64×10 6 m/s / 3.51×10 14 m/s 2 = 7.52×10 -9 s
c) The kinetic energy E k of the electron at the lower plate is given by
E k = (1/2) m v f2 = 0.5×9.11×10 -31 (2.64×10 6 ) 2 = 3.17×10 -18 J
Problem 10:
Two electrons are held 3μm apart. When released from rest, what is the velocity of each electron when they are 8μm apart?
Solution to Problem 10:
Let Ep1 be the potential electric energy at rest (distance r = 3μm) and Ep2 be the potential electric energy when they are 5μm apart and moving. The total (potential and kinetic energies) at each position are given by
Et1 = Ep1 + (1/2) m (0)2 = Ep1
Et2 = Ep2 + (1/2) m v2 + (1/2) m v2 = Ep2 + m v2
The formula for electric potential energy due to charges q1 and q2 distant by r is:
Ep = k q1 q2 /r
No external energy is used and no energy is lost, therefore there is a conservation of energy such that potential energy is converted into kinetic energy.
Ep1 = Ep2 + m v2
v is the velocity when 8μm apart.
charge of electron = - e = -1.60×10-19C
mass of electron m = 9.109×10-31Kg
m v2 = Ep1 - Ep2 = k×e×e / (3×10-6) - k×e×e / (5×10-6) = 9×109(1.6×10-19)2 [ 1 / (3×10-6) - 1 / (8×10-6) ]
v ≈ 3.48×104 m/s
More References and Links