Resolver Problemas de Circuitos DC

Las leyes de Kirchhoff y Ohm se utilizan para resolver problemas de circuitos DC.
Hay 3 ejemplos; resuélvelos en el orden en que se presentan; esto facilitará su comprensión completa.

Problema 1
Encuentra la corriente \( i \), los voltajes \( V_{R_1} \) y \( V_{R_2} \) en el circuito a continuación dado que la fuente de voltaje \( e = 20 \) Voltios, las resistencias \( R_1 = 100 \; \Omega \) y \( R_2 = 300 \; \Omega \).

Solución al Problema 1
Aplica la ley de voltaje de Kirchhoff al bucle cerrado en el circuito y escribe la ecuación
\( e - V_{R_1} - V_{R_2} = 0 \)     (1)
Usa la ley de Ohm para escribir
\( V_{R_1} = i R_1 \) y \( V_{R_2} = i R_2 \)
Sustituye \( V_{R_1} \) y \( V_{R_2} \) por sus expresiones en la ecuación (1)
\( e - i R_1 - i R_2 = 0 \)
Reordena la anterior para que todos los términos que contienen \( i \) estén en un lado
\( i R_1 + i R_2 = e \)
Factoriza \( i \)
\( i ( R_1 + R_2) = e \)
Resuelve para \( i \)
\( i = \dfrac{e}{R_1 + R_2} \)
Sustituye las cantidades conocidas
\( i = \dfrac{20}{100 + 300} = 0.05 \) A
Calcula \( V_{R_1} \) y \( V_{R_2} \) usando la ley de Ohm
\( V_{R_1} = i R_1 = 0.05 \times 100 = 5 \) V
\( V_{R_2} = i R_2 = 0.05 \times 300 = 15\) V

Problema 2
Dadas las fuentes de voltaje \( e_1 = 20 \) V, \( e_2 = 5 \) V, y las resistencias \( R_1 = 100 \; \Omega \), \( R_2 = 300 \; \Omega \) y \( R_3 = 50 \; \Omega \), encuentra todas las corrientes a través y voltajes a través de las resistencias en el circuito.

Solución al Problema 2
La ley de voltaje de Kirchhoff para los tres bucles \( L_1 \), \( L_2 \) y \( L_3 \) da
Bucle \( L_1 \): \( e_1 - V_{R_1} - V_{R_2} = 0 \)      (1)
Bucle \( L_2 \): \( V_{R_2} + e_2 - V_{R_3 } = 0 \)      (2)
Bucle \( L_3 \): \( e_1 - V_{R_1} + e_2 - V_{R_3 } = 0 \)      (3)

Nota que si sumamos las ecuaciones (1) y (2), obtenemos la ecuación (3). Por lo tanto, cualquier 2 ecuaciones de las 3 se pueden usar para resolver los problemas dados. La tercera no da ninguna información adicional.
Tenemos 3 incógnitas, por lo que necesitamos otra ecuación independiente de las ecuaciones anteriores.
La ley de corriente de Kirchhoff aplicada en el nodo A da
\( i_1 = i_2 + i_3 \)      (4)

Entonces seleccionamos las ecuaciones (1), (2) y (4) para escribir el sistema de ecuaciones
\( e_1 - V_{R_1} - V_{R_2} = 0 \)      (5)
\( V_{R_2} + e_2 - V_{R_3 } = 0 \)      (6)
\( i_1 = i_2 + i_3 \)      (7)

Usa la ley de Ohm para reescribir \( V_{R_1} \) y \( V_{R_2} \) de la siguiente manera
\( V_{R_1} = R_1 i_1 \) y \( V_{R_2} = R_2 i_2\)
Sustituye las anteriores en las ecuaciones (5) y (6) y reescribe el sistema de ecuaciones (5), (6) y (7) como
\( R_1 i_1 + R_2 i_2 = e_1 \)      (8)
\( R_2 i_2 - R_3 i_3 = - e_2 \)      (9)
\( i_1 = i_2 + i_3 \)      (10)

Sustituye las cantidades conocidas por sus valores numéricos para obtener un sistema de ecuaciones lineales con tres incógnitas \( i_1 \), \( i_2\) y \( i_3 \) .
\( 100 i_1 + 300 i_2 = 20 \)      (11)
\( 300 i_2 - 50 i_3 = - 5 \)      (12)
\( i_1 = i_2 + i_3 \)      (13)
Hay muchas maneras de resolver el sistema anterior.
Una forma es usar la ecuación (13) y sustituir \( i_1 \) por \( i_2 + i_3 \) en las ecuaciones (11) y (12)
\( 100 (i_2 + i_3) + 300 i_2 = 20 \)
\( 300 i_2 - 50 i_3 = - 5 \)
Resolviendo la primera se obtiene
\( 100 i_2 + 100 i_3 = 20 \)      (14)
Sustituyendo en la segunda
\( 300 i_2 - 50 i_3 = - 5 \)
Reorganizando se obtiene
\( 300 i_2 + 50 i_3 = 5 \)      (15)
Resolvamos el sistema de ecuaciones formado por (14) y (15)
Multiplicando la (14) por \( 5 \) y la (15) por \( 1 \):
\( 500 i_2 + 500 i_3 = 100 \)      (16)
\( 300 i_2 + 50 i_3 = 5 \)      (17)
Restando (17) de (16)
\( 200 i_2 + 450 i_3 = 95 \)      (18)
Resuelve \( i_2 \) y \( i_3 \) y finalmente encuentra \( i_1 \).

Problema 3
Encuentra todas las corrientes a través y voltajes a través de los resistores en el circuito a continuación, dadas las fuentes de voltaje \( e_1 = 20 \) V, \( e_2 = 5 \) V, y las resistencias \( R_1 = 100 \; \Omega \), \( R_2 = 120 \; \Omega \), \( R_3 = 60 \; \Omega \), \( R_4 = 40 \; \Omega \), \( R_5 = 240\; \Omega \) y \( R_6 = 80 \; \Omega \).


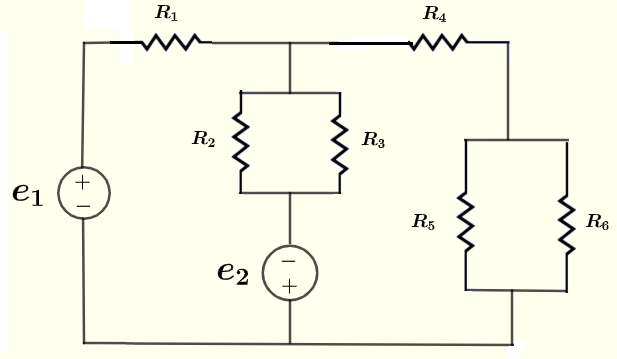
Solución al Problema 3
Todos los detalles de la solución se presentan y, para hacer esta presentación clara y fácil de entender, la solución de este ejemplo tiene 5 partes.

Parte 1: Simplificar el circuito agrupando resistores
Si aplicamos la ley de Kirchhoff a los bucles cerrados y nodos en el circuito dado arriba, terminaremos con un gran número de ecuaciones que resolver.
Sin embargo, un análisis rápido del circuito dado muestra que algunos de los resistores están en configuraciones en paralelo y en serie, como se muestra a continuación.
Los resistores \( R_2 \) y \( R_3 \) están en paralelo y su resistencia equivalente es \( R'_2 \) como se muestra en el circuito a continuación.
\( R_5\) y \( R_6 \) están en paralelo y su resistencia equivalente está en serie con \( R_4 \) y su resistencia equivalente total es \( R'_3 \) como se muestra en el circuito a continuación.

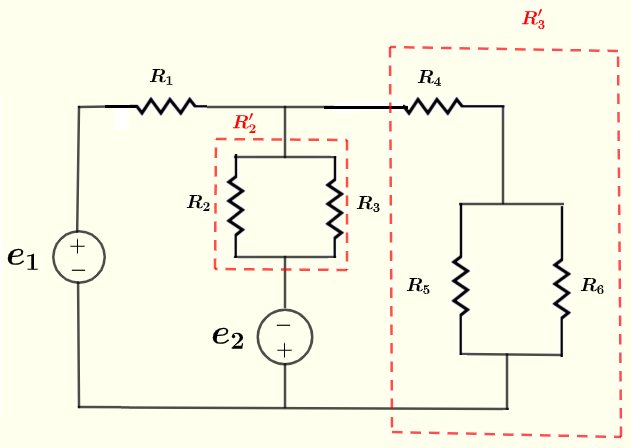
Usa la fórmula para resistores en paralelo para escribir
\( \dfrac{1}{R'_2} = \dfrac{1}{R_2} + \dfrac{1}{R_3} \)
Resuelve la anterior para \( R'_2 \) para obtener
\( R'_2 = \dfrac{R_2 \cdot R_3}{R_2 + R_3} \)
Sustituye las cantidades conocidas para obtener
\( R'_2 = \dfrac{120 \cdot 60}{120 + 60} = 40 \; \Omega \)
Usa la fórmula para resistores en paralelo para \( R_5\) y \( R_6 \) y súmala a \( R_4 \) para escribir \( R'_3 \) como
\( R'_3 = R_4 + \dfrac{R_5 \cdot R_6}{R_5 + R_6} \)
Sustituye las cantidades conocidas para obtener
\( R'_3 = 40 + \dfrac{240 \cdot 80}{240 + 80} = 100\)

Parte 2: Calcular \( i_1 \), \( i_2 \) e \( i_3 \) usando la ley de Kirchhoff
Ahora tenemos un circuito mucho más simple para resolver, como se muestra a continuación.


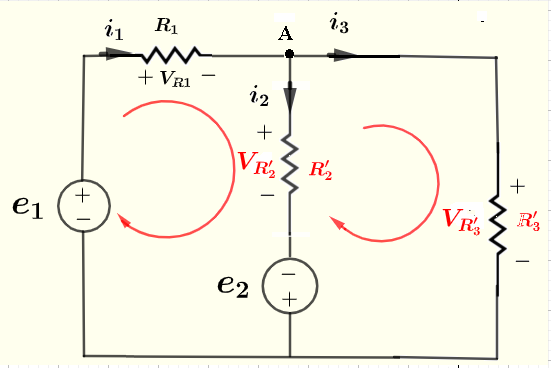
Hay 3 incógnitas \( i_1 \), \( i_2 \) y \( i_3 \), y por lo tanto necesitamos 3 ecuaciones.
Usa la ley de corriente de Kirchhoff en el nodo A para escribir
\( i_1 = i_2 + i_3 \)      (1)
Usa la ley de voltaje de Kirchhoff para el bucle de la izquierda
\( e_1 - V_{R_1} - V_{R'_2} + e_2 = 0 \)      (2)
Usa la ley de voltaje de Kirchhoff para el bucle de la derecha
\( - e_2 + V_{R'_2} - V_{R'_3} = 0 \)      (3)
Usa la ley de Ohm para escribir
\( V_{R_1} = R_1 i_1 \)
\( V_{R'_2} = R'_2 i_2 \)
\( V_{R'_3} = R'_3 i_3 \)
Sustituye los voltajes anteriores en las ecuaciones (2) y (3) e incluye la ecuación (1) para reescribir el sistema de 3 ecuaciones con 3 incógnitas
\( e_1 - R_1 i_1 - R'_2 i_2 + e_2 = 0 \)
\( - e_2 + R'_2 i_2 - R'_3 i_3 = 0 \)
\( i_1 = i_2 + i_3 \)
Sustituye las cantidades conocidas, simplifica y reescribe el sistema anterior en la forma.
\( 100 i_1 + 40 i_2 = 25\)      (4)
\( 40 i_2 - 100 i_3 = 5 \)      (5)
\( i_1 = i_2 + i_3 \)      (6)
Hay muchas maneras de resolver sistemas de ecuaciones lineales. Usaremos el método de sustitución.
Sustituye \( i_1 \) por \( i_2 + i_3 \) en las ecuaciones (4) y reescribe las ecuaciones (4) y (5) como sigue
\( 100 (i_2 + i_3) + 40 i_2 = 25\)      (7)
\( 40 i_2 - 100 i_3 = 5 \)      (8)
Simplifica y agrupa
\( 140 i_2 + 100 i_3 = 25\)
\( 40 i_2 - 100 i_3 = 5 \)
Suma las ecuaciones anteriores para eliminar \( i_3 \)
\( 180 i_2 = 30 \)
Resuelve para \( i_2 \)
\( i_2 = 30/180 = 1/6 \) A
Usa la ecuación (7) (o (8) ) para encontrar \( i_3 \)
\( 100 i_3 = 25 - 140 i_2 \)
\( i_3 = 1/60 \) A
Usa la ecuación (6) para encontrar \( i_1 \)
\( i_1 = i_2 + i_3 = 1/6 + 1/60 = 11/60\)

Parte 3: Calcular corrientes en los resistores \( R_2 \) y \( R_3 \)

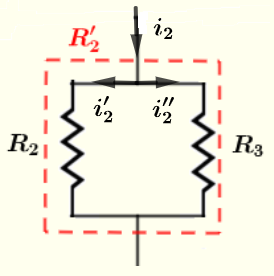
Aplica la ley de corriente de Kirchhoff
\( i_2'+i_2'' = i_2 = 1/6 \)
La ley de voltaje de Kirchhoff al bucle cerrado.
\( R_2 i_2' - R_3 i_2'' = 0 \)
Sustituye las cantidades conocidas en la ecuación anterior
\( 120 i_2' - 60 i_2'' = 0 \)
Resuelve el sistema de 2 ecuaciones con 2 incógnitas
\( i_2'+i_2'' = 1/6 \)
\( 120 i_2' - 60 i_2'' = 0 \)
para obtener
\( i_2' = 1/18 \) A
y \( i_2'' = 1/9 \) A

Parte 4: Calcular corrientes en los resistores \( R_5 \) y \( R_6 \)
Ahora calculamos las corrientes a través de los resistores \( R_5 \) y \( R_6 \) usando el circuito a continuación


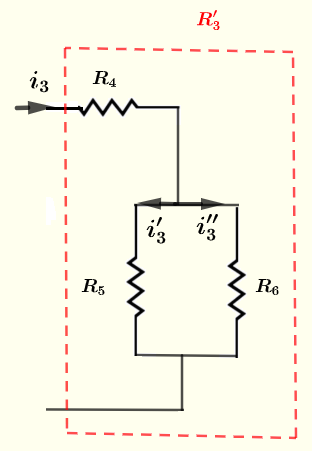
Aplica la ley de corriente de Kirchhoff
\( i_3'+i_3'' = i_3 = 1/60 \)
La ley de voltaje de Kirchhoff al bucle cerrado.
\( R_5 i_3' - R_6 i_3'' = 0 \)
Sustituye las cantidades conocidas en la ecuación anterior
\( 240 i_3' - 80 i_3'' = 0 \)
Resuelve el sistema de 2 ecuaciones con 2 incógnitas
\( i_3'+i_3'' = 1/60 \)
\( 240 i_3' - 80 i_3'' = 0 \)
para obtener
\( i_3' = 1/240 \) A
y \( i_3'' = 1/80 \) A

Parte 5: Calcular voltajes en todos los resistores
Ahora enumeramos todos los resistores y las corrientes a través de cada uno de ellos; y luego calculamos los voltajes a través de cada uno de ellos.
\( R_1 = 100 \; \Omega \), corriente \( i_1 = 11/60 \) A     voltaje : \( V_{R_1} = 100 \times 11/60 = 18.33 \) V
\( R_2 = 120 \; \Omega \), corriente \( i_2' = 1/18 \) A     voltaje : \( V_{R_2} = 120 \times 1/18 = 6.67 \) V
\( R_3 = 60 \; \Omega \), corriente \( i_2'' = 1/9 \) A     voltaje : \( V_{R_3} = 60 \times 1/9 = 6.67 \) V
\( R_4 = 40 \; \Omega \), corriente \( i_3 = 1/60 \) A     voltaje : \( V_{R_4} = 40 \times 1/60 = 0.67 \) V
\( R_5 = 240\; \Omega \), corriente \( i_3' = 1/240 \) A     voltaje : \( V_{R_5} = 240 \times 1/240 = 1 \) V
\( R_6 = 80 \; \Omega \), corriente \( i_2'' = 1/80 \) A     voltaje : \( V_{R_6} = 80 \times 1/80 = 1 \) V

Más referencias y enlaces