Solución
a)
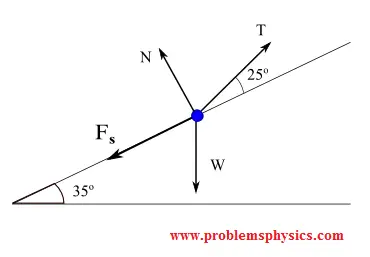
Diagrama de Cuerpo Libre

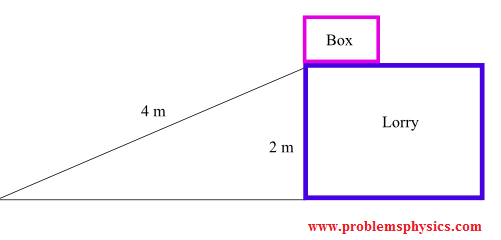
Supongamos que el pequeño punto azul es la caja
Dos fuerzas actúan sobre la caja: el peso W de la caja y N la fuerza normal y ejercida por el plano inclinado sobre la caja (punto azul).
b)
Use el sistema de ejes x-y como se muestra para escribir todas las fuerzas en su
forma de componentes

Vectores N, W y a en forma de componentes:
N = (0 , |N|)
W = (Wx , Wy) = (|W| cos (27°) , - |W| sin (27°))
a = (ax , ay) = (|a| , 0), la caja se mueve hacia abajo en el plano inclinado en la dirección de x positiva, por lo tanto, ay = 0.
Use la segunda ley de Newton para escribir que la suma de todas las fuerzas sobre la caja es igual a la masa por la aceleración (ecuación vectorial).
W + N = M a, M es la masa de la caja.
En forma de componentes, la ecuación anterior se convierte en
(|W| sin (27°) , - |W| cos (27°)) + (0 , |N|) = M (|a| , 0)
Para que dos vectores sean iguales, sus componentes deben ser iguales. Entonces
Los componentes x son iguales: |W| sin (27°) + 0 = M |a|
Los componentes y son iguales: - |W| cos (27°) + |N| = 0
M |a| = |W| sin (27°)
Peso: |W| = M g; g = 10 m/s2
|a| = M g sin (27°) / M = g sin (27) m/s^2 ≈ 4.5 m/s^2
c)
|N| = |W| cos (27°) = 2 × 10 cos (27°) ≈ 17.8 N