Desplazamiento y Distancia: Tutoriales con Ejemplos
Ejemplos con explicaciones sobre desplazamiento y distancia de objetos que se mueven a lo largo de líneas rectas. Más problemas y sus soluciones se pueden encontrar en este sitio.
Definiciones de Distancia y Desplazamiento
La distancia es una cantidad escalar (magnitud) que describe la longitud total del trayecto recorrido por un objeto en movimiento.
El desplazamiento es una cantidad vectorial (magnitud y dirección) que describe la diferencia entre las posiciones final e inicial de un objeto en movimiento. Es la distancia más corta movida en una dirección determinada. Tanto la distancia como el desplazamiento se miden en unidades de longitud (centímetros, metros, kilómetros,...).
Ejemplos con Soluciones Detalladas
Ejemplo 1
Un objeto se mueve de A a D a lo largo del camino rojo como se muestra a continuación.
a) Encuentra la distancia total recorrida por el objeto.
b) Encuentra el desplazamiento del objeto.
 Solución:
Solución:
a) Usando la escala dada (1 km por división), la distancia total d se da por
d = AB + BC + CD = 2 + 5 + 2 = 9 km
b) Se usan las posiciones inicial y final del objeto en movimiento para encontrar el desplazamiento. La distancia de A (posición inicial) a D (posición final) es igual a AD = 5 km.
El desplazamiento es el vector AD cuya magnitud es de 5 km y su dirección es hacia el este.
Ejemplo 2
Un objeto se mueve, a lo largo de una línea, desde el punto A al punto B al punto C y luego de vuelta al punto B como se muestra en la figura a continuación.
a) Encuentra la distancia recorrida por el objeto en movimiento.
b) Encuentra la magnitud del desplazamiento del objeto.
 Solución:
Solución:
a) La distancia total d recorrida por el objeto es
d = AB + BC + CB = 5 km + 4 km + 4 km = 13 km
b) La magnitud del desplazamiento es igual a la distancia de A (posición inicial) a B (posición final), que es igual a 5 km.
Ejemplo 3
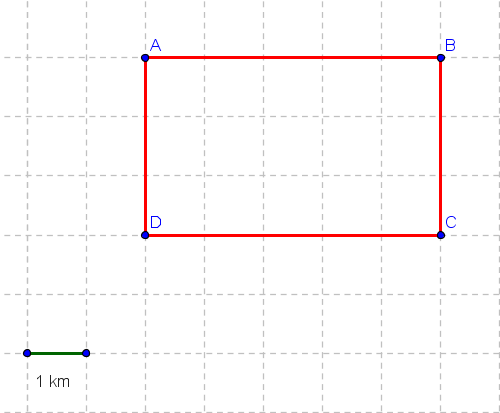
Un objeto se mueve desde el punto A al punto B al punto C al punto D y luego de regreso a A a lo largo del rectángulo que se muestra en la figura a continuación.
a) Encuentra la distancia total recorrida por el objeto en movimiento.
b) Encuentra el desplazamiento del objeto.
 Solución:
Solución:
a) La distancia total d es igual al perímetro del rectángulo. Usando la escala dada,
d = 2 AB + 2 BC = 10 + 6 = 16 km
b) Dado que el objeto en movimiento comienza en el punto A y termina en A, no hay cambio en la posición del objeto y, por lo tanto, el desplazamiento es igual a cero.
Ejemplo 4
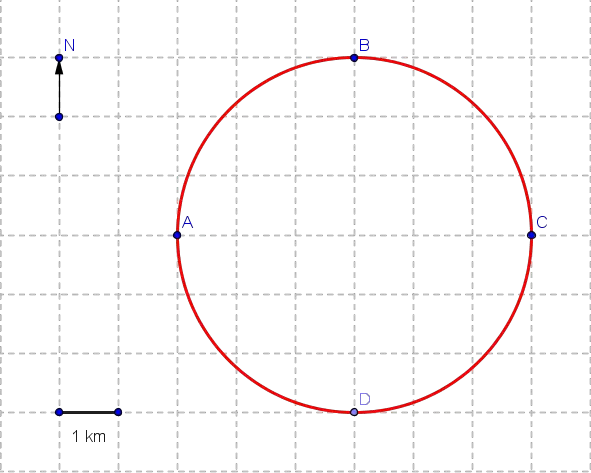
Un objeto se mueve del punto A al punto B al punto C a lo largo del círculo como se muestra en la figura a continuación.
a) Encuentra la distancia total recorrida por el objeto en movimiento.
b) Encuentra el desplazamiento del objeto.
 Solución:
Solución:
a) La distancia total d es igual a la mitad de la circunferencia del círculo y se da por
d = (1/2)(2 * Pi * 3) = 3 Pi km
b) La magnitud del desplazamiento D es igual al diámetro AC del círculo y se da por
D = 2 * 3 = 6 km con dirección hacia el este.
Ejemplo 5
Un objeto se mueve desde el punto A hasta el punto B a lo largo del círculo como se muestra en la figura a continuación.
a) Encuentra la distancia total recorrida por el objeto en movimiento.
b) Encuentra la magnitud del desplazamiento del objeto.
 Solución:
Solución:
a) La distancia total d es igual a un cuarto de la circunferencia del círculo y se da por
d = (1/4)(2 * Pi * 3) = 1.5 Pi km
b) La magnitud del desplazamiento D es igual a la hipotenusa AB del ángulo recto ABO como se muestra a continuación
 Usa el teorema de Pitágoras para encontrar AB de la siguiente manera
Usa el teorema de Pitágoras para encontrar AB de la siguiente manera
AB2 = 32 + 32 = 18
D = AB = 3√2 km
Más Referencias y Enlaces
 Solución:
Solución:
 Solución:
Solución:
 Solución:
Solución:
 Solución:
Solución:
 Usa el teorema de Pitágoras para encontrar AB de la siguiente manera
Usa el teorema de Pitágoras para encontrar AB de la siguiente manera