p = m v
k = (1/2) m v2
M = 2 m y V = 2 v (masa y velocidad duplicadas)
P = M V = (2m)(2v) = 4 m v el momento se cuadruplica.
K = (1/2) M V2 = (1/2) (2 m) (2 v) 2 = (1/2) 8 m v2 : la energía cinética se multiplica por 8
Respuesta: D
Momentos iguales
|p1| = m1 |v1| y |p2| = m2 |v2| , magnitud de los momentos de los objetos A y B
Sea K1 = (1/2) m1 |v1|2 y K2 = (1/2) m2 |v2|2 , las energías cinéticas de los objetos A y B
Sabemos que
|v1| < |v2|
Multiplicamos ambos lados de la desigualdad por (1/2) |p1| y (1/2) |p2| tomando en cuenta que |p1| = |p2|
(1/2) |p1| |v1| < (1/2) |p2| |v2|
Sustituyendo |p1| y |p2| por sus expresiones obtenidas arriba
(1/2) m1 |v1| |V1| < (1/2) m2 |v2| |v2|
lo que da
K1 < K2
La energía cinética de B es mayor que la de A
Respuesta: D
Energías cinéticas iguales
K1 = (1/2) m1 |v1|2, K2 = (1/2) m2 |v2|2, las energías cinéticas de los objetos A y B son iguales
K1 = K2 dado
Sea |p1| = m1 |v1| y |p2| = m2 |v2|, los momentos de los objetos A y B
Sabemos que
|v1| < |v2|
Dividir el numerador y el denominador en lo anterior por K1 y K2 (nota K1 = K2), para obtener
|v1| / K1 < |v2| / K2
Lo que da
K1 / |v1| > K2 / |v2|
Sustituir K1 y K2 por sus expresiones dadas arriba
(1/2) m1 |v1|2 / |v1| > (1/2) m2 |v2|2 / |v2|
Simplificar para obtener
m1 |v1| > m2 |v2|
Lo que da |p1| > |p2|
Respuesta: B
Los frenos en un coche se utilizan para detener el coche y, por lo tanto, cambiar el momento del coche de algún valor a cero. La relación entre una fuerza aplicada a un objeto de masa m y el cambio de su momento en física se da por
F Δt = Δp = m (vf - vi), vf es la velocidad final y vi la velocidad inicial, Δ t es el tiempo durante el cual se aplica la fuerza F.
en magnitud
|F| Δ t = m |vf - vi|, asumiendo que vf y vi están en la misma dirección o en direcciones opuestas.
Δ t
Δ t = 2000 |0 - 35| / 4000 = 17.5 segundos
Respuesta: E
Momento antes de la colisión: m1 v1 + m2 v2
Momento después de la colisión: (m1 + m1)(1/2)(v1 + v2)
El momento se conserva: m1 v1 + m2 v2 = (m1 + m1)(1/2)(v1 + v2)
Multiplicar todos los términos por 2, expandir y simplificar
m1 v1 - m1 v2 + m2 v2 - m2 v1 = 0
factorizar
m1 (v1 - v2) - m2 (v1 - v2) = 0
(m1 - m2)(v1 - v2) = 0
Teniendo en cuenta que v1 no es igual a v2, resolver la ecuación anterior para obtener
m1 = m2
Respuesta: D
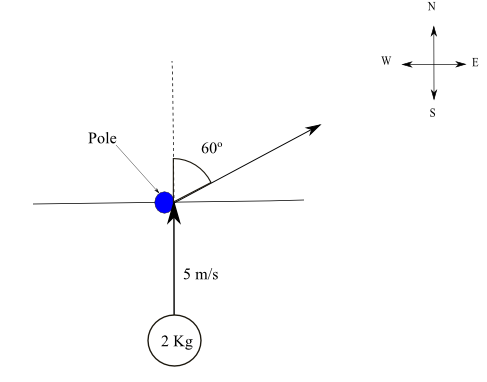
Momento antes de golpear el poste: p1 = m v = 2 × 5 = 10 K.m/s un componente (solo) hacia el norte
Momento después de golpear el poste: 2 componentes: hacia el norte p2n = 2 × 5 cos (60°), hacia el este: p2e = 2 × 5 sin (60°)
Cambio en la magnitud de los componentes: p2n - p1 = 2 × 5 cos (60°) - p1 = 5 - 10 = - 5 Kg.m/s
Respuesta: C
Momento antes de la colisión: p1 = 4×6 + 6×5 = 54 Kg.m/s
Momento después de la colisión: p2 = (4 + 6) v2; v2 es la velocidad de los dos objetos juntos después de la colisión
El momento se conserva: 54 = 10 v2
v2 = 5.4 m/s
Energía cinética antes de la colisión: K1 = (1/2) (4) 62 + (1/2) (6) 52 = 147 J
Energía cinética después de la colisión: K2 = (1/2) (4 + 6) 5.42 = 145.8 J
Cambio en la energía cinética: K2 - K1 = 145.8 - 147 = - 1.2 J
Se perdió 1.2 J de energía cinética.
Respuesta: A
Momento antes de la colisión: p1 = 0 Kg.m/s (ambos objetos en reposo)
Asumimos que un objeto que se mueve hacia la derecha se mueve en la dirección positiva.
Momento después de la colisión: p2 = 1 (-9) + 3 (v2) = - 9 + 3 v2; v2 es la velocidad del objeto B
El momento se conserva: 0 = - 9 + 3 v2
v2 = 3 m/s y B se mueve hacia la derecha
Respuesta: B
Respuesta: D
Asumiendo movimiento positivo cuando un objeto se mueve hacia la derecha. Dado que ambos objetos se mueven a lo largo de una línea recta, las velocidades tienen un componente a lo largo de la trayectoria de movimiento que es una línea recta y este componente es positivo (hacia la derecha) o negativo (hacia la izquierda).
Momento antes de la colisión: p1 = m1 |v1| - m2 |v2|, |v2| es la magnitud del objeto B.
Momento después de la colisión: p2 = 0 (ambos se detienen, por lo tanto, las velocidades son iguales a 0 después de la colisión).
Conservación del momento: m1 |v1| - m2 |v2| = 0
Resolver para |v2|
|v2| = |v1| (m1 / m2)
Respuesta: B