Principios y Aplicaciones de Lentes Ópticas
Contenido de la Página
Refracción de Rayos de Luz en Diferentes Situaciones
Primero necesitamos entender la refracción de rayos de luz para examinar cómo funcionan las lentes convexas y cóncavas.
Estudiaremos el ángulo de desviación del rayo refractado con respecto a la normal en la interfaz. Consideramos un rayo de luz que incide sobre un medio con índice de refracción n1 hacia un medio con índice de refracción n2.
Consideraremos 3 casos diferentes: n1 < n2, n1 > n2 y el caso especial donde el ángulo de incidencia es igual a 0.
caso 1) n1 < n2
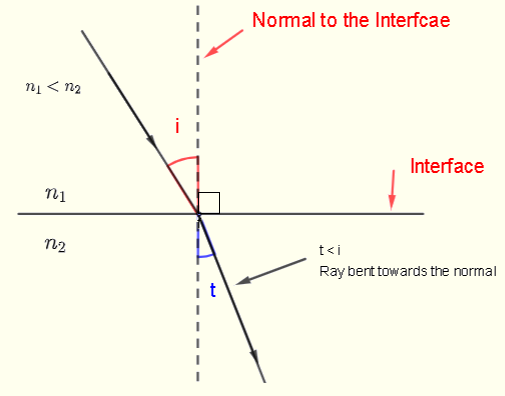
De acuerdo con la ley de Snell tenemos
n1 sin(i) = n2 sin (t)
lo que puede escribirse como
(n1 / n2) sin(i) = sin (t)
n1 < n2 puede escribirse como n1 / n2 < 1
Multiplicamos todos los términos de la desigualdad anterior por sin(i) para obtener
(n1 / n2) sin(i) < sin(i)
Sustituimos (n1 / n2) sin(i) por sin(t) para obtener
sin(t) < sin(i)
Lo que da: t < i
Lo que significa que el ángulo t es menor que el ángulo i, o el rayo refractado se dobla hacia la normal de la interfaz. Así que al pasar de un material con menor densidad óptica a un material con mayor densidad óptica, el rayo se refracta hacia la normal de la interfaz. (Ver diagrama a continuación)
caso 2) n1 > n2
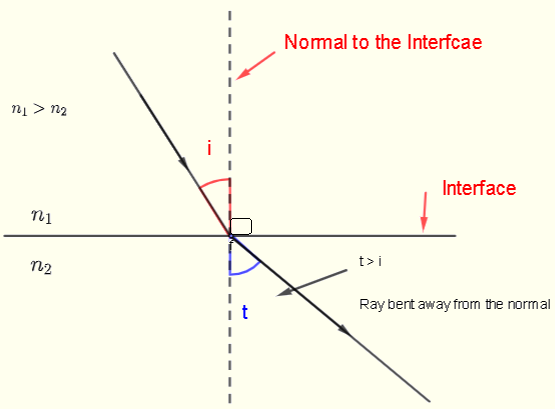
De acuerdo con la ley de Snell tenemos
(n1 / n2) sin(i) = sin (t)
(ver arriba)
n1 > n2 puede escribirse como
n1 / n2 > 1
Multiplicamos todos los términos de la desigualdad anterior por sin(i) para obtener
(n1 / n2) sin(i) > sin(i)
Sustituimos (n1 / n2) sin(i) por sin(t) para obtener
sin(t) > sin(i)
Lo que da: t > i
Lo que significa que el ángulo t es mayor que el ángulo i, o el rayo refractado se dobla alejándose de la normal de la interfaz. Al pasar de un material más denso ópticamente a uno menos denso, el rayo se refracta alejándose de la normal.
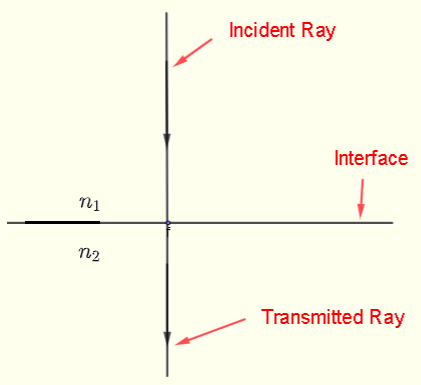
caso 3) ángulo de incidencia i es igual a 0
El rayo se transmite en el medio 2 con un ángulo igual a cero, como se muestra a continuación.
Ejemplo 1
En el diagrama de abajo, un rayo de luz incide en el medio (1) y viaja a través de diferentes medios. El camino del rayo indica que el ángulo de refracción aumenta desde el medio (1) hasta el medio (5).
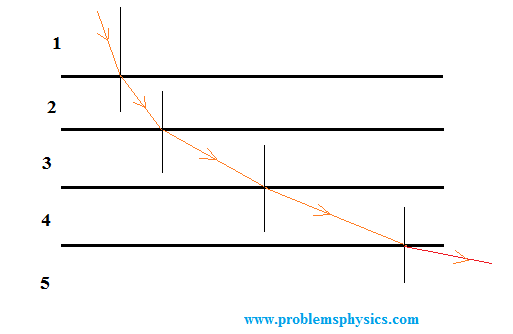
a) ¿Qué medio tiene el índice de refracción más bajo?
b) ¿Qué medio tiene la velocidad de la luz más baja?
Solución
a)
Primero, el ángulo de refracción en el medio (2) es mayor que el ángulo de incidencia en el medio (1). Por lo tanto, el índice de refracción del medio (1) es mayor que el índice de refracción del medio (2). A medida que avanzamos del medio (2) al medio (5), el ángulo de refracción aumenta. Por lo tanto, el índice de refracción disminuye del medio (1) al medio (5). El medio (5) tiene el índice de refracción más bajo.
b)
El índice de refracción n de un medio se define como la razón entre la velocidad de la luz en el vacío c (constante) y la velocidad de la luz v en el medio.
n = c / v
v = c / n
Según la parte a) anterior, el medio (1) tiene el índice de refracción más alto y, por lo tanto, el medio (1) tiene la velocidad de la luz más baja de acuerdo con la fórmula v = c / n anterior.
Principios de Lentes Convergentes
En la figura de abajo, un rayo de luz horizontal incide en el aire sobre el lado AB de un trozo triangular de vidrio. El índice de refracción del vidrio (más denso ópticamente) es mayor que 1 (índice de refracción del aire, menos denso ópticamente), por lo que el rayo se refracta hacia (ángulo r) la normal en AB en el punto M. Una segunda refracción en el punto N, donde el rayo pasa del vidrio (más denso ópticamente) al aire (menos denso ópticamente), refractará el rayo alejándose de la normal en BC en N con una desviación general del rayo desde la dirección original (horizontal) hacia abajo.
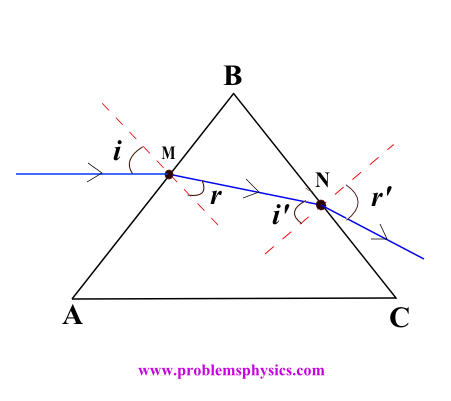
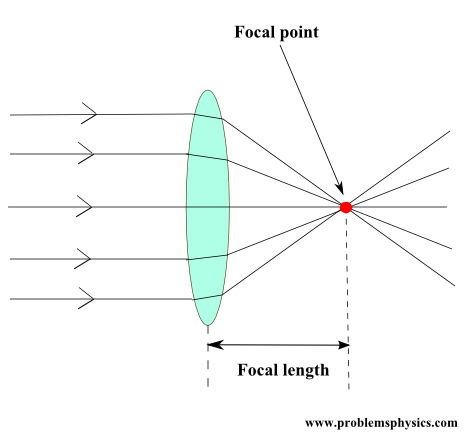
Basado en lo anterior, es posible diseñar un trozo de vidrio con una forma tal que refracte muchos rayos entrantes paralelos a su eje que convergerían hacia un punto común llamado punto focal (foco), como se muestra a continuación. Esto se llama una lente convexa convergente. (ver abajo)
Principios de Lentes Divergentes
En la figura de abajo, el rayo incidente entrante en AB se refracta hacia la normal (de medios menos densos ópticamente a más densos ópticamente) y se aleja de la dirección horizontal. Una segunda refracción en N refractará el rayo alejándose de la normal (de medios más densos ópticamente a menos densos ópticamente) en N y por lo tanto, más lejos y arriba de la dirección (horizontal) del rayo original.
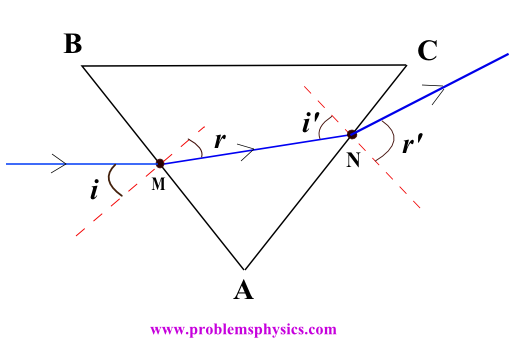
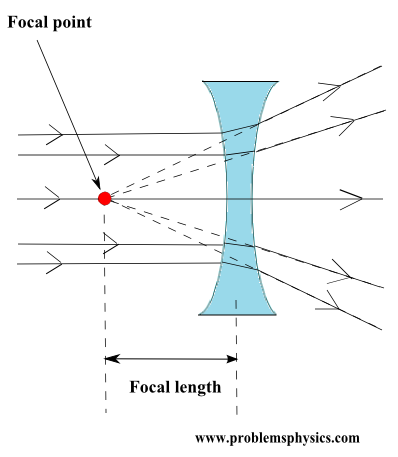
Basado en lo anterior, es posible diseñar un trozo de vidrio con una forma tal que refracte muchos rayos entrantes paralelos (a su eje) que se desviarían de la dirección horizontal como se muestra a continuación. Esto se llama lente cóncava divergente (ver abajo).
Aplicaciones de Lentes Ópticas
Las lentes ópticas se encuentran o se utilizan en
- nuestros ojos
- telescopios astronómicos
- binoculares
- lupas
- microscopios
- gafas y lentes de contacto
Más Referencias y Enlaces
- Ley de Snell
- https://books.google.ca/books/about/Principles_of_Optics_and_Refraction.html?id=Vi-uAAAAIAAJ&redir_esc=y - Principios de Óptica - Por Max Born, Emil Wolf
- Cambridge University Press, 19 de diciembre de 2019.
- Óptica e Instrumentos Ópticos – Por B. K. Johnson - Noviembre de 2011
- Introducción al Diseño de Lentes – Tapa dura – Por José Sasián - 26 de septiembre de 2019







