Calculadoras de Corrientes y Voltajes en Circuitos DC
\( \) \( \)\( \) \( \)
Se presentan tres calculadoras en línea para calcular todas las corrientes y voltajes en tres circuitos DC diferentes. Practica resolviendo circuitos DC manualmente y verifica las respuestas usando estas calculadoras.
1 - Fórmulas de Voltajes y Corrientes en el Circuito 1
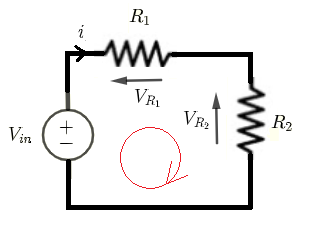 Dado \( V_{in} \), \( R_1 \) y \( R_2 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \) y \( R_2 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Usando las leyes de Kirchhoff de voltajes para escribir las ecuaciones:
\( V_{in} = R_1 i + R_2 i \) (I)
Resolvemos para \( i \)
\( i = \dfrac{V_{in}}{R_1 + R_2} \)
Usamos la ley de Ohm para encontrar los voltajes:
\( V_{R_1} = i R_{1} = \dfrac{ R_{1} V_{in}}{R_1 + R_2} \)
\( V_{R_2} = i R_{2} = \dfrac{ R_{2} V_{in}}{R_1 + R_2} \)
Calculadora de Voltajes y Corrientes para el Circuito 2
Ingresa la fuente de voltaje \( V_{in} \) en voltios y las resistencias \( R_1\) y \( R_4 \) en \( \Omega \) y presiona "Calcular". La calculadora usa las fórmulas anteriores para calcular todas las corrientes y voltajes cuyas fórmulas se obtuvieron anteriormente.
Resultados
2 - Fórmulas de Voltajes y Corrientes en el Circuito 2
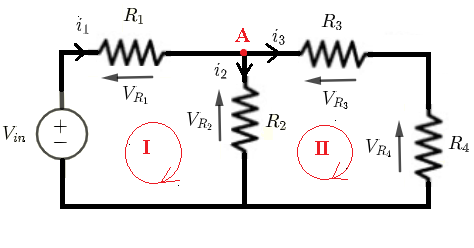 Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \) y \( R_4 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \) y \( R_4 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Usando las leyes de Kirchhoff de voltajes para escribir las ecuaciones:
Lazo (I): \( V_{in} = R_1 i_1 + R_2 i_2 \) (I)
Lazo (II): \( - R_2 i_2 + R_3 i_3 + R_4 i_3 = 0 \) (II)
Usando las leyes de Kirchhoff de corrientes para escribir la ecuación:
Nodo (A): \( i_1 = i_2 + i_3 \) (III)
Sustituyendo \( i_1 \) por \( i_2 + i_3 \) en las ecuaciones (I) y reordenando las ecuaciones (I) y (II), obtenemos un sistema de dos ecuaciones con dos incógnitas \( i_2 \) e \( i_3 \)
\( (R_1 + R_2) i_2 + R_1 i_3 = V_{in} \)
\( - R_2 i_2 + (R_3 + R_4) i_3 = 0 \)
Usa cualquier método para resolver el sistema de ecuaciones y obtener
\( i_2 = \dfrac{R_3 + R_4}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( i_3 = \dfrac{R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
Usa la ecuación (III) para encontrar \( i_1 \)
\( i_1 = i_2+i_3 = \dfrac{R_2+R_3 + R_4}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
Los voltajes en las resistencias están dados por la ley de Ohm de la siguiente manera:
\( V_{R_1} = R_1 i_1 = \dfrac{R_1(R_2 + R_3 + R_4)}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_2} = R_2 i_2 = \dfrac{R_2(R_3 + R_4)}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_3} = R_3 i_3 = \dfrac{R_3 R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
\( V_{R_4} = R_4 i_3 = \dfrac{R_4 R_2}{(R_1 + R_2)(R_3+R_4)+R_1R_2} V_{in} \)
Calculadora de Voltajes y Corrientes para el Circuito 2
Introduce la fuente de voltaje \( V_{in} \) en voltios y las resistencias \( R_1, R_2, R_3 \) y \( R_4 \) en \( \Omega \) y presiona "Calcular". La calculadora utiliza las fórmulas anteriores para calcular todas las corrientes y voltajes cuyas fórmulas se obtuvieron previamente.
Resultados
3 - Fórmulas de Voltajes y Corrientes en el Circuito 3
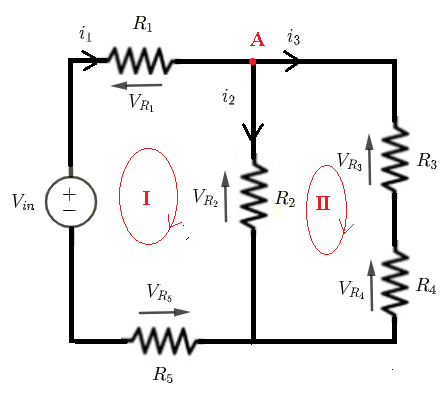 Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \), \( R_4 \) y \( R_5 \), vamos a encontrar las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \), \( R_4 \) y \( R_5 \), vamos a encontrar las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Usando las leyes de Kirchhoff de voltajes para escribir las ecuaciones:
Lazo (I): \( V_{in} = R_1 i_1 + R_2 i_2 + R_5 i_1 \) (I)
Lazo (II): \( - R_2 i_2 + R_3 i_3 + R_4 i_3 = 0 \) (II)
Usando las leyes de Kirchhoff de corrientes para escribir la ecuación:
Nodo (A): \( i_1 = i_2 + i_3 \)
La ecuación (I) obtenida de las leyes de Kirchhoff para el circuito 2 es:
\( V_{in} = R_1 i_1 + R_2 i_2 \)
La ecuación (I) obtenida de las leyes de Kirchhoff para el circuito 3 es:
\( V_{in} = R_1 i_1 + R_2 i_2 + R_5 i_1 = (R_1 + R_5) i_1 + R_2 i_2 \)
La única diferencia es que el coeficiente de \( i_1 \) es \( R_1 + R_5 \) en el circuito 3 y \( R_1 \) en el circuito 2. Por lo tanto, no necesitamos resolver el sistema de tres ecuaciones desde el principio, solo sustituimos \( R_1 \) en las soluciones para el circuito 2 por \( R_1 + R_5 \) para obtener las soluciones del circuito 3 que son:
\( i_1 = \dfrac{R_2+R_3 + R_4}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( i_2 = \dfrac{R_3 + R_4}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( i_3 = \dfrac{R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
Los voltajes a través de las resistencias están dados por:
\( V_{R_1} = R_1 i_1 = \dfrac{R_1(R_2+R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_2} = R_2 i_2 = \dfrac{R_2(R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_3} = R_3 i_3 = \dfrac{R_3 R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_4} = R_4 i_3 = \dfrac{R_4 R_2}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
\( V_{R_5} = R_5 i_1 = \dfrac{R_5(R_2+R_3 + R_4)}{(R_1 + R_5 + R_2)(R_3+R_4)+(R_1 + R_5) R_2} V_{in} \)
Calculadora de Voltajes y Corrientes para el Circuito 3
Introduce la fuente de voltaje \( V_{in} \) en voltios y las resistencias \( R_1, R_2, R_3, R_4\) y \( R_5 \) en \( \Omega \) y presiona "Calcular". La calculadora utiliza las fórmulas anteriores para calcular todas las corrientes y voltajes cuyas fórmulas se obtuvieron anteriormente.
Resultados
Más Referencias y Enlaces
Ley de Ohm con Ejemplos
Soluciones Gratuitas para el SAT II Física sobre
Circuitos Eléctricos DC
 Dado \( V_{in} \), \( R_1 \) y \( R_2 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \) y \( R_2 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
 Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \) y \( R_4 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \) y \( R_4 \), encontremos las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
 Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \), \( R_4 \) y \( R_5 \), vamos a encontrar las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.
Dado \( V_{in} \), \( R_1 \), \( R_2 \), \( R_3 \), \( R_4 \) y \( R_5 \), vamos a encontrar las fórmulas para las corrientes a través de y los voltajes en todas las resistencias.