Calculadora de Divisor de Voltaje DC
Se presenta una calculadora en línea para calcular el voltaje de salida, la corriente y la potencia de una carga en un divisor de voltaje de corriente continua. Se sugieren actividades utilizando la calculadora para investigar la potencia máxima entregada a la carga \( R_L \).
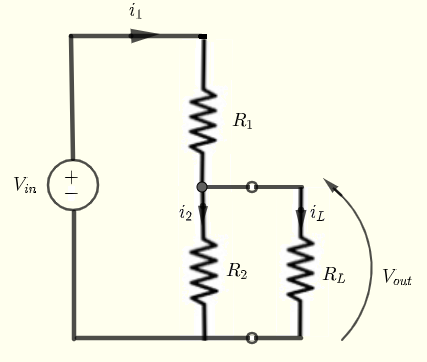
Fórmulas de Corriente, Voltaje y Potencia
Dado \( V_{in} \), \( R_1 \), \( R_2 \) y la carga \( R_L \), vamos a encontrar las fórmulas para la corriente \( i_L \) a través de la carga, el voltaje \( V_L \) sobre la carga y la potencia entregada a la carga (resistor) \( R_L \).
Utilizando las leyes de Kirchhoff de voltaje y corriente, podemos escribir las siguientes ecuaciones:
\( V_{in} = R_1 i_1 + R_2 i_2 \) (I)
\( - R_2 i_2 + R_L i_L = 0 \) (II)
\( i_1 = i_2 + i_L \) (III)
Sustituyendo \( i_1 \) en la ecuación (I) por \( i_2 + i_L \), obtenemos dos ecuaciones con dos incógnitas \( i_2 \) y \( i_L \)
\( V_{in} = R_1 (i_2 + i_L) + R_2 i_2 \) (I')
\( - R_2 i_2 + R_L i_L = 0 \) (II')
Resuelve el sistema de dos ecuaciones y dos incógnitas por cualquier método para obtener
\( i_L = \dfrac{R_2}{R_L(R_1+R_2)+R_1 R_2} V_{in} \)
Utiliza la Ley de Ohm para encontrar \( V_L \):
\( V_L = R_L i_L = \dfrac{R_2 R_L}{R_L(R_1+R_2)+R_1 R_2} V_{in} \)
La potencia \( P_L \) entregada a la carga se da por
\( P_L = V_L i_L \)
Calculadora de Divisor de Voltaje DC
Ingrese las resistencias de \( R_1 \), \( R_2 \), \( R_L \) en Ohmios y el voltaje de la fuente \( V_{in} \) en voltios como números reales positivos y presione "Calcular". Los resultados son la corriente \( i_L \) a través de \( R_L \), el voltaje \( V_L \) sobre \( R_L \) y la potencia \( P_L \) entregada a la carga \( R_L \).
Resultados
Actividades
Se puede demostrar que cuando \( R_L = \dfrac{R_1 R_2}{R_1 + R_2} \), la potencia entregada a la carga \( R_L \) es máxima.
Seleccione valores para \( R_1 \) y \( R_2 \), y calcule \( R_L \) utilizando la fórmula \( R_L = \dfrac{R_1 R_2}{R_1 + R_2} \), e ingrese todos los valores en la calculadora para calcular \( P_L \).
Luego mantenga los valores de \( R_1 \) y \( R_2 \) constantes pero cambie ligeramente \( R_L \) por encima o por debajo del valor calculado. ¿Qué valor de \( R_L \) da el valor máximo de \( P_L \)?
Ejemplo
Sea \( R_1 = 20 \) y \( R_2 = 30 \), por lo tanto \( R_L = \dfrac{20 \times 30}{20 + 30} = 12 \)
Ingrese los valores \( R_1 = 20 \), \( R_2 = 30 \) y \( R_L = 12 \) en la calculadora.
¿Cuál es el valor de \( P_L \)?
Mantenga \( R_1 = 20 \) y \( R_2 = 30 \), pero cambie \( R_L \) a valores diferentes de 12, como valores superiores (13, 14, 15, ...) o inferiores (11, 10, 9 ...), y anote los valores de \( P_L \).
¿Qué valor de \( R_L \) da el valor más alto de \( P_L \)?
Más Referencias y Enlaces
Ley de Ohm con Ejemplos
Ley de Kirchhoff para Circuitos con Ejemplos
Electricidad
Soluciones Gratuitas de Pruebas de Práctica SAT II Física sobre
Circuitos Eléctricos DC

