Una partícula se mueve 80 cm al sur en 0.12 segundos y luego 60 cm al oeste en 0.08 segundos. ¿Cuál es la magnitud de la velocidad promedio de la partícula?
A) 700 cm/s
B) 1417 cm/s
C) 500 cm/s
D) 250 cm/s
E) 709 cm/s
Solución
Para encontrar la velocidad promedio, necesitamos el desplazamiento y el tiempo. La trayectoria de la partícula sigue los dos lados de un triángulo rectángulo, por lo tanto, la magnitud del desplazamiento $d$ es la hipotenusa del triángulo rectángulo con lados de $80$ y $60$. Usamos el teorema de Pitágoras:
$\text{d}^2=80^2+60^2$, lo que da d = $100$ cm
$\text{velocidad} = \dfrac{\text{desplazamiento}}{\text{tiempo}} = \dfrac{100 cm}{0.12 s + 0.08 s} = 500 $ cm/s
Cuando la velocidad de un coche cambia de 20 m/s a 40 m/s, su energía cinética
A) permanece igual
B) se duplica
C) se reduce a la mitad
D) se triplica
E) se cuadruplica
Solución
La energía cinética E de una partícula que tiene velocidad constante v y masa m está dada por:
$E=\dfrac{1}{2}mv^2$
En este caso, la velocidad cambia de 20 a 40 m/s, por lo tanto, se duplica.
Si duplicamos v en la fórmula de E, obtenemos:
$E' = \dfrac{1}{2}m(2v)^2 = 2mv^2$
La energía se multiplica por 4, por lo tanto, se cuadruplica.
El siguiente gráfico muestra la velocidad de una partícula en movimiento. ¿En cuál de los puntos A, B, C, D o E la aceleración es mayor?

A) A
B) B
C) C
D) D
E) E
Solución
La aceleración es el cambio de velocidad sobre el tiempo, por lo tanto, un cambio más grande en la velocidad v significa una aceleración mayor. Si examinamos el gráfico dado, la velocidad v cambia rápidamente en el punto A (la tangente en ese punto es la más pronunciada) y, por lo tanto, la aceleración es mayor en el punto A.
El siguiente gráfico muestra la altura de una pelota lanzada verticalmente hacia arriba. ¿En qué punto la velocidad está cerca o igual a cero?

A) A
B) B
C) C
D) D
E) E
Solución
La velocidad es el cambio de altura con respecto al tiempo. En el punto C, no hay cambio en la altura (la tangente en ese punto es horizontal y su pendiente es igual a cero). Por lo tanto, la velocidad está cerca o es igual a cero en el punto C.
Los capacitores entre A y B y C y D son equivalentes y tienen una capacitancia C cada uno. ¿Cuántos capacitores equivalentes, con capacitancia C, necesitamos poner en serie entre E y F para que la capacitancia total en el circuito sea igual a 2.5C?

A) 2
B) 3
C) 4
D) 5
E) 6
Solución
Sea Ceq la capacitancia de los capacitores entre el punto E y F. Entonces tenemos 3 capacitores en paralelo cuya capacitancia equivalente está dada por C + C + Ceq, que es igual a 2.5C. Por lo tanto, Ceq = 0.5C
Si ahora ponemos n capacitores de capacitancia C en serie entre E y F, tenemos:
1 / Ceq = 1/C + 1/C + 1/C + ... + 1/C = n/C
Ceq = C/n
Ceq = 0.5C = C/n
n = 2
Todos los resistores en el circuito siguiente son equivalentes. ¿Cuál es la relación entre la caída de voltaje entre los puntos A y B y la caída de voltaje entre los puntos B y C?

A) 1/3
B) 1/9
C) 1/6
D) 1/2
E) 1
Solución
Todos los resistores son equivalentes y, por lo tanto, tienen la misma resistencia R. Tres resistores en serie son equivalentes a 3R. Sea Req el resistor equivalente a los grupos de resistores 3R entre B y C, entonces tenemos:
1 / Req = 1/3R + 1/3R + 1/3R = 3/3R = 1/R
Por lo tanto, Req = R
Así que los resistores entre A y B y entre B y C son equivalentes y, por lo tanto, la caída de voltaje entre A y B y entre B y C es igual, por lo que su relación es igual a 1
Los vectores u y v tienen magnitudes de 15 y 7 unidades respectivamente. ¿Cuál es el valor máximo posible de la magnitud del vector 3u - 2v?
A) 31 unidades
B) 45 unidades
C) 66 unidades
D) 59 unidades
E) 8 unidades
Solución
La magnitud del vector 3u es igual a 3*15 = 45 y la magnitud de -2v es igual a 2*7 = 14
La magnitud es máxima cuando los vectores 3u y -2v son paralelos y opuestos, en cuyo caso la magnitud de 3u - 2v = 45 + 14 = 59
Para aumentar la frecuencia de las oscilaciones, para pequeñas amplitudes, de un péndulo de longitud L con una bola de masa M, necesitas
A) aumentar L
B) disminuir L
C) aumentar M
D) disminuir M
E) disminuir tanto M como L
Solución
El período T de un péndulo de longitud L está dado por
$T=2\pi\sqrt{\dfrac{L}{g}}$
Si F es la frecuencia, entonces $F = 1/T = \dfrac{1}{2\pi}\sqrt{\dfrac{g}{L}}$
Para aumentar F, debemos disminuir L.
¿Cuál es la tensión en la cuerda superior del sistema compuesto por dos bloques de metal, cada uno de 5 kg, suspendidos del techo por cuerdas de masa despreciable, como se muestra a continuación?

A) 49 N
B) 25 N
C) 980 N
D) 98 N
E) 10 N
Solución
La tensión $T$ en la cuerda superior es la fuerza ejercida por la cuerda para mantener el equilibrio. Por lo tanto, la magnitud de $T$ es igual al peso de ambas masas:
$T = 5\cdot g + 5\cdot g = 98$ N
En la figura siguiente, se muestra una masa M unida a un resorte. La posición inicial de la masa M está en el punto C. A y B son las posiciones extremas de la masa mientras oscila. La energía cinética de la masa M es máxima en

A) solo en el punto A
B) solo en el punto B
C) solo en el punto C
D) en los puntos A y B
E) en los puntos C y B
Solución
En los puntos A y B, la masa se detiene para cambiar de dirección, y por lo tanto, la velocidad en cada uno de estos dos puntos es igual a cero, lo que significa que la energía cinética en estos puntos es cero (la energía potencial es máxima). En el punto C, toda la energía potencial se ha convertido en energía cinética, por lo tanto, la energía cinética es máxima en el punto C.
¿Cuál es el componente en y de la fuerza resultante cuando 3 fuerzas, cuyas magnitudes se dan, actúan sobre un objeto en el punto O, como se muestra en la figura?
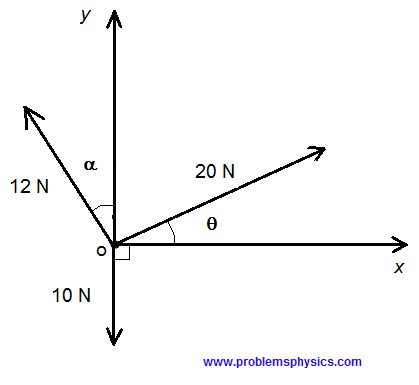
A) 12 cos(α) + 20 sin(θ)
B) 12 sin(α) + 20 sin(θ)
C) -10
D) 12 sin(α) + 20 sin(θ) - 10
E) 12 cos(α) + 20 sin(θ) - 10
Solución
Calculemos el componente x $x_c$ y el componente y $y_c$ de cada fuerza:
Fuerza de 20 N: $x_c = 20 cos(\theta)$ ; $y_c = 20 sin(\theta)$
Fuerza de 12 N: $x_c = -12 sin(\alpha)$ ; $y_c = 12 cos(\alpha)$
Fuerza de 10 N: $x_c = 0$ ; $y_c = -10$
El componente y de la fuerza resultante es la suma de los 3 componentes y de las fuerzas que actúan, y está dado por
$20 sin(\theta) + 12cos(\alpha) - 10$
El gráfico de la velocidad contra el tiempo de un objeto en movimiento se muestra a continuación. ¿Cuál es el desplazamiento entre t = 3 y t = 5?

A) 4 m
B) 2 m
C) igual o cercano a cero
D) -4 m
E) -2 m
Solución
El desplazamiento entre t = 3 y t = 5 es el área total de la superficie entre la curva de v y el eje x, teniendo en cuenta que el área de una superficie debajo del eje es negativa y el área de una superficie sobre el eje x es positiva. Por lo tanto, el área del triángulo de t = 3 a t = 4 es igual a (1/2)*2*1 = 1, y el área del triángulo de t = 4 a t=5 es igual a -(1/2)*2*1 = -1, y la suma de ambas áreas es igual a cero.
Tres partículas con cargas +q en los puntos A, -q en el punto B y +q en el punto C están ubicadas en los vértices de un triángulo equilátero, y la línea a través de A y B es paralela al eje x. ¿Qué es cierto acerca de la fuerza resultante que actúa sobre la carga en el punto C?

A) sus componentes en x e y son iguales
B) su componente en y es igual a cero
C) su componente en x es igual a cero
D) sus componentes en x e y son iguales a cero
E) su dirección forma un ángulo de 45 grados con el eje x
Solución
Las dos fuerzas que actúan sobre la carga en el punto C se muestran a continuación. Debido a que los lados de un triángulo equilátero son iguales, y las cargas son iguales en magnitud, la magnitud de todas las fuerzas que actúan sobre C es igual. Dado que AB es paralelo al eje x, los ángulos que forman las dos fuerzas que actúan en C con el eje x son iguales en magnitud y de signos opuestos, por lo que el componente vertical de la fuerza resultante es igual a cero. Todas las demás afirmaciones sobre la resultante son incorrectas. Respuesta B.

¿Cuál es el momento de un objeto en movimiento que tiene una masa de 100 Kg y una energía cinética de 20,000 Julios?
A) 10,000 Kg.m/s
B) 100 Kg.m/s
C) 1000 Kg.m/s
D) 2000,000 Kg.m/s
E) 2000 Kg.m/s
Solución
La energía cinética está dada por $\dfrac{1}{2}mv^2 = 20,000$ y $m=100$ se puede usar para encontrar $v^2=400$ y $v=20$ m/s
Por lo tanto, el momento $p = mv = 100 Kg * 20$ m/s $= 2,000$ Kg.m/s
La bola $A$ de masa $m$ y velocidad $v$ choca con la bola $B$ de masa m y velocidad $-v$. ¿Cuáles son las velocidades $V_A$ y $V_B$ de las dos bolas después de la colisión?
A) $V_A=-v$ y $V_B=v$
B) $V_A=v$ y $V_B=-v$
C) $V_A=-v$ y $V_B=-v$
D) $V_A=v$ y $V_B=v$
E) $V_A=0$ y $V_B=v$
Solución
El momento de las dos bolas antes de la colisión está dado por $mv + m(-v) = 0$. Sean $V_A$ y $V_B$ las velocidades de A y B después de la colisión, ya que el momento se conserva, podemos escribir $mv+m(-v)=mV_A + mV_B$, lo que se simplifica a $mV_A + mV_B=0$, lo que da $V_A = -V_B$
La conservación de la energía cinética da: $\dfrac{1}{2}mv^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}mV_A^2+\dfrac{1}{2}mV_B^2$
Sustituye $V_B$ por $-V_A$ arriba y simplifica a $v^2 = V_A^2$
lo que da $V_A=\pm v$
Dado que la bola A irá en la dirección opuesta después de la colisión, $V_A=-v$ y $V_B=v$
La distancia entre dos crestas sucesivas de una onda es de $10^{-12}$ metros. El tiempo entre la llegada de crestas sucesivas es igual a $10^{-11}$ segundos. ¿Cuál es la velocidad de la onda?
A) 100 m
B) 0.1 mm
C) 10 cm
D) 10 mm
E) 1 km
Solución
La distancia entre dos crestas es igual a la longitud de onda de la onda y el período de tiempo entre dos crestas sucesivas es el período de la onda. La velocidad v está dada por $v =\dfrac {longitud\ de\ onda}{período}= \dfrac{10^{-12}m}{10^{-11}s} = 0.1 m/s = 10 cm/s$
¿Cuál es la fuerza gravitatoria, redondeada al Newton más cercano, sobre un satélite de masa 100 kilogramos en una órbita h de 38,400 kilómetros? (El radio R de la Tierra es aproximadamente igual a 6,400 kilómetros)
A) 27 N
B) 980 N
C) 1000 N
D) 163 N
E) 6000 N
Solución
Sea $m_1$ la masa del satélite. La fuerza gravitatoria $F_1$ del satélite sobre la Tierra está dada por $F_1=\dfrac{Gm_1m_2}{R^2}=m_1*g=100*9.8=980 N$
La fuerza gravitatoria $F_2$ del satélite a h = 38,400 km está dada por $F_2=\dfrac{Gm_1m_2}{h^2}$
La relación entre las dos fuerzas
$\dfrac{F_2}{F_1} = \dfrac{\dfrac{Gm_1m_2}{h^2}}{\dfrac{Gm_1m_2}{R^2}} = \dfrac{R^2}{h^2}=\dfrac{38,400}{6,400}=\dfrac{1}{36}$
$F_2=\dfrac{980}{36}=27 N$ (redondeado)
¿Qué le sucederá a la presión de un gas en un recipiente cerrado si su temperatura (en grados Kelvin) se duplica?
A) se reduce a la mitad
B) se duplica
C) se mantiene igual
D) disminuye
E) se cuadruplica
Solución
Para un volumen fijo, la presión es proporcional a la temperatura. Si la temperatura se duplica, la presión también se duplica.
Un rayo de luz incide en un ángulo de $21.8^o$ en la interfaz entre un material con índice de refracción $n_1$ y un material con índice de refracción $n_2$ como se muestra en la figura a continuación. ¿Cuál es la medida del ángulo $x$ que el rayo emergente forma con la perpendicular a la segunda interfaz? (Suponga que las interfaces son paralelas)

A) $\dfrac{n_1}{n_2}21.8^o$
B) $\dfrac{n_2}{n_1}21.8^o$
C) $43.6^o$
D) $45^o$
E) $21.8^o$
Solución
Aplica la ley de Snell en cada interfaz.
$n_1 sin(21.8^o)=n_2 \sin(A)$ (interfaz a la izquierda)
$n_2 sin(B) = n_1 \sin(x)$ (interfaz a la derecha)
A es el ángulo de refracción en la interfaz (izquierda) $n_1 - n_2$ y B es el ángulo de incidencia en la interfaz (derecha) $n_2 - n_1$. Los ángulos A y B son iguales ya que las interfaces son paralelas.
lo que da $n_1\sin(21.8) = n_1\sin(x)$ y $x=21.8^o$
¿Cuál es la energía de un fotón con frecuencia $2.0 \times 10^{17}$Hz? (constante de Planck $h = 6.6 \times 10^{-34}$J.s)
A) $3.3 \times 10^{-51}$ J
B) $6.6 \times 10^{-51}$ J
C) $1.32 \times 10^{-17}$ J
D) $1.32 \times 10^{-16}$ J
E) $8.6 \times 10^{-17}$ J
Solución
La energía $e$ de un fotón con frecuencia f está dada por
$e=hf=2.0 \times 10^{17} \cdot 6.6 \times 10^{-34}=1.32 \times 10^{-16}$ J