Problemas de cargas y fuerzas electrostáticas se presentan junto con sus soluciones detalladas.
Problema 1:
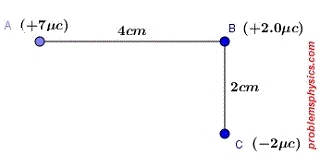
¿Cuál es la fuerza neta y su dirección que las cargas en los vértices A y C del triángulo rectángulo ABC ejercen sobre la carga en el vértice B?


Problema 2:
Una carga positiva q ejerce una fuerza de magnitud - 0.20 N sobre otra carga - 2q. Encuentra la magnitud de cada carga si la distancia que las separa es igual a 50 cm.
Solución al Problema 2:
La fuerza que q ejerce sobre 2q está dada por la ley de Coulomb:
F = k (q) ( - 2q) / r2,
Dado: r = 0.5 m , F = - 0.20 N,
Usa la fórmula de F anterior para escribir la ecuación
- 0.2 = - 2 q2 k / 0.52
k es la constante de Coulomb (k ≈ 9 × 109 )
Resuelve para q2
q2 = 0.2 × 0.52 / (2 k)
q = √ [ (0.2 × 0.52 / (2 × 9 × 109) ] = 1.66 × 10-6 C
Las dos cargas son:
q = 1.66 × 10-6 C,
-2 q = -3.23 × 10-6 C
Problema 3:
Dos objetos idénticos, separados por una distancia d, con cargas de igual magnitud pero de signos opuestos, ejercen una fuerza de atracción de - 2.5 N entre sí. ¿Qué fuerza ejercen estos objetos entre sí si la distancia entre ellos se convierte en 2d?
Solución al Problema 3:
Sea q y -q las dos cargas. La magnitud de la fuerza que q y -q, separadas por una distancia d, ejercen entre sí está dada por la ley de Coulomb:
F = k (q) (- q) / d2 = - k q2 / d2 = - 2.5 N
La magnitud de la fuerza F2 que q y -q, separadas por una distancia 2d, ejercen entre sí está dada por la ley de Coulomb:
F2 = k (q) (- q) / (2 d)2 = - k q2 / 4 d2 = F / 4 = - 2.5 / 4 = - 0.625 N
Problema 4:
Una carga de q = - 4.0 × 10-6 se coloca en un campo eléctrico y experimenta una fuerza de 5.5 N [E].
a) ¿Cuál es la magnitud y dirección del campo eléctrico en el punto donde se encuentra la carga q?
b) Si se retira la carga q, ¿cuál es la magnitud y dirección de la fuerza ejercida sobre una carga de - 2q en el mismo lugar donde estaba la carga q?
Solución al Problema 4:
a) La fuerza sobre una carga q debido a un campo eléctrico E está dada por
F = q E
La magnitud de E está dada por
| E | = | F | / | q | = 5.5 / (4.0 × 10-6) = 1.375 × 106 N / C
Dado que la carga q es negativa, F y E tienen direcciones opuestas. E es 1.375 × 106 N / C [O].
b) La fuerza sobre una carga -2q debido a un campo eléctrico E está dada por
F2 = -2 q E = -2(q E) = -2(5.5[E]) = -11 [E] o 11 N [O].
Problema 5:
Tres cargas están ubicadas en los vértices de un triángulo isósceles rectángulo como se muestra a continuación. ¿Cuál es la magnitud y la dirección del campo eléctrico resultante en el punto medio M de AC?


Problema 6:
¿Qué distancia debe separar dos cargas de + 5.6×10-4C y -6.3×10-4 C para que la energía potencial eléctrica en el sistema de las dos cargas tenga una magnitud de 5.0 J?
Solución al Problema 6:
La magnitud de la energía potencial eléctrica Ep de un sistema de dos cargas q1 y q2 separadas por una distancia r está dada por
Ep = k | q1 | | q2 | / r.
Resuelve para r:
r = k q1 q2 / Ep = 9.00×109×5.6×10-4×6.3×10-4 / 5.0 = 6.35×102 m.
Problema 7:
La distancia entre dos cargas q1 = + 2 μC y q2 = + 6 μC es de 15.0 cm. Calcula la distancia desde la carga q1 hasta los puntos en el segmento de línea que une las dos cargas donde el campo eléctrico es cero.
Solución al Problema 7:
A una distancia x de q1, el campo eléctrico total es la suma vectorial del campo E1 debido a q1 dirigido a la derecha y el campo eléctrico E2 debido a q2 dirigido a la izquierda. La suma vectorial es igual a cero si las magnitudes de los dos campos E1 y E2 son iguales, ya que tienen direcciones opuestas.

Problema 8:
La distancia AB entre las cargas Q1 y Q2 mostradas a continuación es de 5.0 m. ¿Cuánto trabajo debe realizarse para mover la carga Q2 a una nueva ubicación en el punto C, de modo que la distancia BC sea de 2.5 m?

Problema 9:
Dos placas paralelas separadas por una distancia de 1 cm tienen una diferencia de potencial de 20 V entre ellas. Las placas se mantienen en una posición horizontal, con la placa negativa sobre la placa positiva. Se libera un electrón desde el reposo en la placa superior.
a) ¿Cuál es la aceleración del electrón?
b) ¿Cuánto tiempo tarda en llegar a la placa inferior?
c) ¿Cuál es la energía cinética del electrón cuando golpea la placa inferior?
Nota: carga del electrón q = -1.6×10-19C, masa del electrón m = 9.11×10-31Kg
Solución al Problema 9:

Problema 10:
Dos electrones se mantienen separados a 3μm. Cuando se liberan desde el reposo, ¿cuál es la velocidad de cada electrón cuando están separados por 8μm?
Solución al Problema 10:
Sea Ep1 la energía potencial eléctrica en reposo (distancia r = 3μm) y Ep2 la energía potencial eléctrica cuando están separados por 5μm y en movimiento. Las energías totales (potencial y cinética) en cada posición están dadas por:
Et1 = Ep1 + (1/2) m (0)2 = Ep1
Et2 = Ep2 + (1/2) m v2 + (1/2) m v2 = Ep2 + m v2
La fórmula para la energía potencial eléctrica debida a las cargas q1 y q2 separadas por r es:
Ep = k q1 q2 / r
No se usa energía externa ni se pierde energía, por lo tanto, hay una conservación de la energía, de modo que la energía potencial se convierte en energía cinética.
Ep1 = Ep2 + m v2
v es la velocidad cuando están separados por 8μm.
carga del electrón = - e = -1.60×10-19C
masa del electrón m = 9.109×10-31Kg
m v2 = Ep1 - Ep2 = k×e×e / (3×10-6) - k×e×e / (5×10-6) = 9×109(1.6×10-19)2 [ 1 / (3×10-6) - 1 / (8×10-6) ]
v ≈ 3.48×104 m/s