
Se presentan algunas de las fórmulas más importantes para vectores, como la magnitud, la dirección, el vector unitario, suma, resta, multiplicación escalar y producto cruzado.
Los componentes de un vector \( \vec {PQ} \) definido por dos puntos \( P(P_x \;, \; P_y \;, \; P_z )\) (punto inicial) y \( Q(Q_x \;, \; Q_y \;, \; Q_z )\) (punto terminal) son los siguientes: \[ \vec{PQ} = \;< Q_x - P_x \;, \; Q_y - P_y \;, \; Q_z - P_z > \]
En lo que sigue, \( \vec A, \vec B \) y \( \vec C \) son vectores tridimensionales dados por sus componentes de la siguiente manera:
\( \vec A = \; < A_x \;, \; A_y \;, \; A_z > \)
\( \vec B = \; < B_x \;, \; B_y \;, \; B_z > \)
\( \vec C = \; < C_x \;, \; C_y \;, \; C_z > \)
La magnitud del vector \( \vec A \), escrita como \( |\vec A| \), se define por
\[ |\vec A| = \sqrt{A_x^2 + A_y^2 + A_z^2} \]
Un vector unitario es un vector cuya magnitud es igual a 1.
El vector unitario \( \vec u \) que tiene la misma dirección que el vector \( \vec A \) se da por:
\[ \vec u = \dfrac{\vec A}{|\vec A|} = \; < \dfrac{A_x}{\sqrt{A_x^2 + A_y^2 + A_z^2}} \;, \; \dfrac{A_y}{\sqrt{A_x^2 + A_y^2 + A_z^2}} \;,\; \dfrac{A_z}{\sqrt{A_x^2 + A_y^2 + A_z^2}} > \]
En un espacio tridimensional, la dirección de un vector se define por tres ángulos \( \alpha \), \( \beta \) y \( \gamma\) (ver Figura 1 a continuación) llamados cosenos directores.

En 2-D, la dirección de un vector se define como un ángulo (ángulo \( \theta \) en la figura a continuación) que un vector forma con el eje positivo x.

La resta de los vectores \( \vec A \) y \( \vec B \) se define por \[ \vec A - \vec B = \; < A_x - B_x \; , \; A_y - B_y \; , \; A_z - B_z > \] Más sobre Resta de Vectores y sumar y restar vectores.
La multiplicación de un vector \( \vec A \) por un escalar \( k \) se define por \[ k \vec A = \; < k A_x \; , \; k A_y \; , \; k A_z > \]
El producto escalar (o producto punto) de dos vectores \( \vec A \) y \( \vec B \) se define por
\[ \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot\cos \theta \]
donde \( \theta \) es el ángulo entre los vectores \( \vec A \) y \( \vec B \).
Dadas las coordenadas de los vectores \( \vec A \) y \( \vec B \), se puede demostrar que
\[ \vec A \cdot \vec B = A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z \]
\[ \vec A \cdot \vec B = \vec B \cdot \vec A \] \[ \vec A \cdot (\vec B + \vec C) = \vec A \cdot \vec B + \vec A \cdot \vec C \] \[ k \vec A \cdot (\vec B)= k (\vec A \cdot \vec B) \]
Dos vectores \( \vec A \) y \( \vec B \) son ortogonales, es decir, el ángulo \( \theta \) entre ellos es igual a \( 90^{\circ} \), si y solo si \[ \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot \cos \theta = |\vec A| \cdot |\vec B| \cdot \cos 90^{\circ} = 0\]
Si \( \theta \) es el ángulo formado por dos vectores \( \vec A \) y \( \vec B \), entonces \[ \cos \theta = \dfrac{\vec A \cdot \vec B}{ |\vec A|\cdot |\vec B|} = \dfrac{A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z}{ \sqrt{A_x^2 + A_y^2 + A_z^2} \cdot\sqrt{B_x^2 + B_y^2 + B_z^2}} \]
El producto cruzado de dos vectores \( \vec A \) y \( \vec B \) es un vector ortogonal a ambos vectores y se define por
\[ \vec A \times \vec B = \begin{vmatrix}
\vec i & \vec j & \vec k\\
A_x & A_y & A_z\\
B_x & B_y & B_z
\end{vmatrix} \\ = (A_y B_z - A_z B_y ) \vec i - (A_x B_z - A_z B_x) \vec j + (A_x B_y - A_y B_x) \vec k\]

\[ \vec A \times \vec B = - \vec B \times \vec A \]
\[ (k \vec A) \times \vec B = \vec A \times (k \vec B ) = k( \vec A \times \vec B) \]
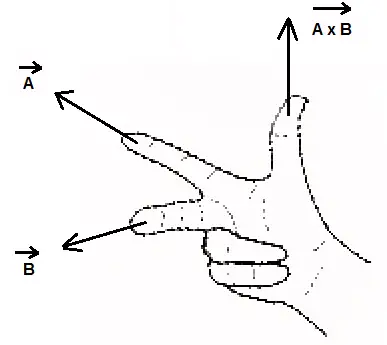
El producto cruzado es un vector, y puede ser necesario, como en electromagnetismo y muchos otros temas de física, encontrar la orientación de este vector. Usa la regla de la mano derecha para encontrar la orientación del producto cruzado: apunta el índice en la dirección del vector A, el dedo medio en la dirección del vector B y la dirección del producto cruzado \( \vec A \times \vec B \) está en la misma dirección del pulgar.
El área de un paralelogramo definido por los vectores \( \vec A \) y \( \vec B \) es la magnitud de su producto cruzado, dada por:
 \[ \text{Área del Paralelogramo} = |\vec A \times \vec B| = |\vec A | \cdot |\vec B| \cdot |\sin \theta|\]
\[ \text{Área del Paralelogramo} = |\vec A \times \vec B| = |\vec A | \cdot |\vec B| \cdot |\sin \theta|\]