Some of the most important formulas for vectors such as the magnitude, the direction, the unit vector, addition, subtraction, scalar multiplication and cross product are presented.
\( \) \( \)\( \) \( \) The components of a vector \( \vec {PQ} \) defined by two points \( P(P_x \;, \; P_y \;, \; P_z )\) (initial point) and \( Q(Q_x \;, \; Q_y \;, \; Q_z )\) (terminal point) are given as follows: \[ \vec{PQ} = \;< Q_x - P_x \;, \; Q_y - P_y \;, \; Q_z - P_z > \]
In what follows \( \vec A, \vec B \) and \( \vec C \) are 3 dimensional vectors given by their components as follows:
\( \vec A = \; < A_x \;, \; A_y \;, \; A_z > \)
\( \vec B = \; < B_x \;, \; B_y \;, \; B_z > \)
\( \vec C = \; < C_x \;, \; C_y \;, \; C_z > \)
The magnitude of vector \( \vec A \) written as \( |\vec A| \) is given by
\[ |\vec A| = \sqrt{A_x^2 + A_y^2 + A_z^2} \]
A unit vector is a vector whose magnitude is equal to 1.
The unit vector \( \vec u \) that has the same direction as vector \( \vec A \) is given by
\[ \vec u = \dfrac{\vec A}{|\vec A|} = \; < \dfrac{A_x}{\sqrt{A_x^2 + A_y^2 + A_z^2}} \;, \; \dfrac{A_y}{\sqrt{A_x^2 + A_y^2 + A_z^2}} \;,\; \dfrac{A_z}{\sqrt{A_x^2 + A_y^2 + A_z^2}} > \]
In 3 dimensional space, the direction of a vector is defined by 3 angles \( \alpha \) , \( \beta \) and \( \gamma\) (see Figure 1. below) called direction cosines.
In 2-D, the direction of a vector is defined as an angle ( angle \( \theta \) in the figure below ) that a vector makes with the positive x-axis.
The subtraction of vectors \( \vec A \) and \( \vec B \) is defined by \[ \vec A - \vec B = \; < A_x - B_x \; , \; A_y - B_y \; , \; A_z - B_z > \] More on vector subtraction and adding and subtracting vectors.
The multiplication of a vector \( \vec A \) by a scalar \( k \) is defined by \[ k \vec A = \; < k A_x \; , \; k A_y \; , \; k A_z > \]
The Scalar (or dot) product of two vectors \( \vec A \) and \( \vec B \) is given by
\[ \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot\cos \theta \]
where \( \theta \) is the angle between vectors \( \vec A \) and \( \vec B \).
Given the coordinates of vectors \( \vec A \) and \( \vec B \), it can be shown that
\[ \vec A \cdot \vec B = A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z \]
\[ \vec A \cdot \vec B = \vec B \cdot \vec A \] \[ \vec A \cdot (\vec B + \vec C) = \vec A \cdot \vec B + \vec A \cdot \vec C \] \[ k \vec A \cdot (\vec B) = k (\vec A \cdot \vec B) \]
Two vectors \( \vec A \) and \( \vec B \) are orthogonal, the angle \( \theta \) between equal to \( 90^{\circ} \), if and only if \[ \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot \cos \theta = |\vec A| \cdot |\vec B| \cdot \cos 90^{\circ} = 0\]
If \( \theta \) is the angle made by two vectors \( \vec A \) and \( \vec B \), then \[ \cos \theta = \dfrac{\vec A \cdot \vec B}{ |\vec A|\cdot |\vec B|} = \dfrac{A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z}{ \sqrt{A_x^2 + A_y^2 + A_z^2} \cdot\sqrt{B_x^2 + B_y^2 + B_z^2}} \]
The cross product of two vectors \( \vec A \) and \( \vec B \) is a vector orthogonal to both vectors and is given by
\[ \vec A \times \vec B = \begin{vmatrix}
\vec i & \vec j & \vec k\\
A_x & A_y & A_z\\
B_x & B_y & B_z
\end{vmatrix} \\ = (A_y B_z - A_z B_y ) \vec i - (A_x B_z - A_z B_x) \vec j + (A_x B_y - A_y B_x) \vec k\]
\[ \vec A \times \vec B = - \vec B \times \vec A \]
\[ (k \vec A) \times \vec B = \vec A \times (k \vec B ) = k( \vec A \times \vec B) \]
The cross product is a vector and there may a need as in eletromagnetism and many other topics in physics to find the orientation of this vector. Use the right hand rule to find the orientation of the cross product: point the index in the direction of vector A, the middle finger in the direction of vector B and the direction of the cross product A × B is in the same direction of the thumb.
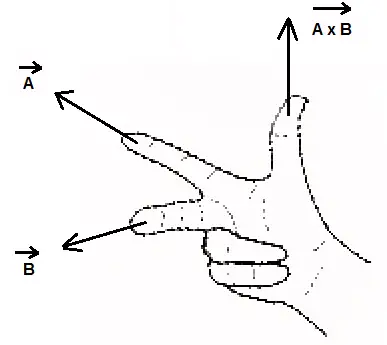
\[ \text{Area of Parallelogram} = |\vec A \times \vec B| = |\vec A | \cdot |\vec B| \cdot |\sin \theta|\]