Consider a light ray incident from a medium with refractive index \(n_1 = 1.1\) to a medium with refractive index \(n_2 = 1.0\). Let \(i\) be the angle of incidence and \(t\) the angle of refraction.

According to Snell's law:
\[ n_1 \sin(i) = n_2 \sin(t) \]
Solving for \(t\):
\[ t = \arcsin\left(\frac{n_1}{n_2} \sin(i)\right) \]
Values for different angles of incidence:
| Angle \(i\) | \(\sin(t) = \frac{n_1}{n_2} \sin(i)\) | \(t = \arcsin\left(\frac{n_1}{n_2} \sin(i)\right)\) |
|---|---|---|
| \(40^\circ\) | 0.70 | \(45.0^\circ\) |
| \(65.39^\circ\) | 1.0 | \(90.0^\circ\) |
| \(75^\circ\) | 1.06 (sine cannot exceed 1) |
No refraction Total reflection occurs |
Since \(n_1 > n_2\), there exists a critical angle \(i_c\) where the refracted angle becomes \(90^\circ\). From the table, \(i_c = 65.39^\circ\). Any incidence angle greater than \(i_c\) results in total internal reflection.

Using Snell's law when \(t = 90^\circ\):
\[ n_1 \sin(i_c) = n_2 \sin(90^\circ) = n_2 \]
Thus:
\[ \sin(i_c) = \frac{n_2}{n_1} \]
\[ i_c = \arcsin\left(\frac{n_2}{n_1}\right) \]
For \(i > i_c\), no refraction occurs—the ray is completely reflected back into medium \(n_1\).
A light ray in water (\(n_1 = 1.3\)) strikes a water-air interface (\(n_2 = 1.0\)) at \(10^\circ\) to the normal.

a) Find the angle of refraction.
b) What incidence angle gives refraction ≤ \(45^\circ\)?
c) Determine the critical angle.
a) Using Snell's law:
\[ 1.3 \sin(10^\circ) = 1.0 \sin(t) \]
\[ t = \arcsin(1.3 \sin(10^\circ)) \approx 13.0^\circ \]
b) For \(t \leq 45^\circ\):
\[ \sin(t) \leq \frac{\sqrt{2}}{2} \]
\[ 1.3 \sin(i) \leq \frac{\sqrt{2}}{2} \]
\[ \sin(i) \leq \frac{\sqrt{2}}{2.6} \]
\[ i \leq \arcsin\left(\frac{\sqrt{2}}{2.6}\right) \approx 33.0^\circ \]
c) Critical angle:
\[ i_c = \arcsin\left(\frac{1.0}{1.3}\right) \approx 50.3^\circ \]
An optical fiber has a glass core (\(n_1 = 1.5\)) surrounded by cladding with lower refractive index \(n_2\).

a) Find \(n_2\) so the core-cladding critical angle is \(80^\circ\).
b) For what ray angles \(\alpha\) with the fiber axis is the incidence angle \(i\) greater than this critical angle?
a) Using the critical angle formula:
\[ \sin(80^\circ) = \frac{n_2}{1.5} \]
\[ n_2 = 1.5 \sin(80^\circ) \approx 1.48 \]
b) Geometry gives \(i = 90^\circ - \alpha\). For total internal reflection:
\[ i > i_c \implies 90^\circ - \alpha > 80^\circ \]
\[ \alpha < 10^\circ \]
Thus, rays within \(10^\circ\) of the fiber axis undergo total internal reflection.
Which paths are possible for light going from \(n_1 = 1.7\) to \(n_2 = 1.0\)?
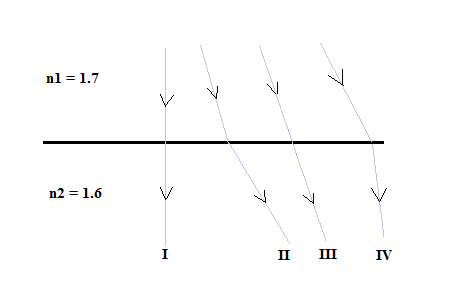
A) I only B) II only C) I and II only D) I, II and IV only E) IV only
Case I (normal incidence): transmission without bending — possible.
Case II (\(n_1 > n_2\)): refraction away from normal — possible.
Cases III & IV show refraction toward normal, which requires \(n_1 < n_2\) — impossible here.
Answer: C