Refraction and Critical Angles Calculator

A calculator that uses Snell's law to calculate the angle of refraction and the critical angle for total internal reflection is presented.
One of the most important parameters that measures optical properties of a medium is the index of refraction (or refractive index). When light rays are incident on a surface separating two media of different indices, there is reflection and refraction of light as shown in the diagram below and Snell's law gives a relationship between the angle of incidence α and angle of refraction β as follows:

n₁ sin α = n₂ sin β

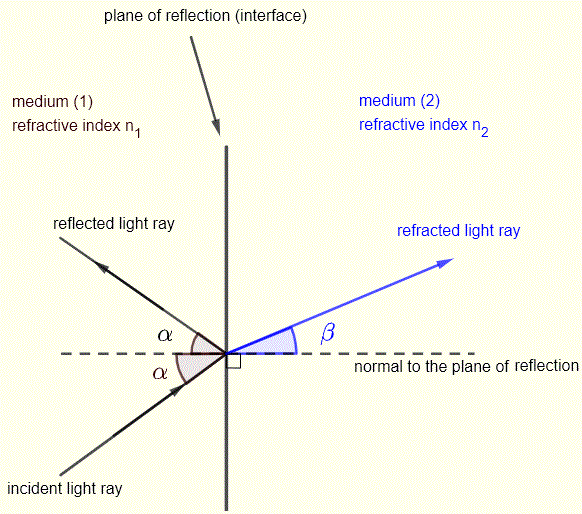
$Incident, reflected and refracted rays$

Using Snell's law given above, we can solve for β to obtain
β = sin^-1(n₁ sin α / n₂)
In many applications, we need total internal reflection of light within medium (1). Optical fibers are examples of systems where total internal reflection of light is used to carry light between distant points. The angle of incidence α_c corresponding to β = 90 � is called the critical angle and is given by Snell's law as follows
n₁ sin α_c = n₂ sin 90�
sin α_c = n₂ / n₁
α_c = sin^-1(n₂ / n₁)
If light rays are incident on a surface separating two media of indices n₁ > n₂, total internal reflection occurs if the angle of incidence α is greter than the critical angle α_c.
This calculator computes the angle of refraction β using Snell's law and the critical angle α_c given above.
NOTE that the critical angle α_c exixts only if n₁ > n₂ and also angle β can be calculated if n₁ sin α / n₂ ≤ 1