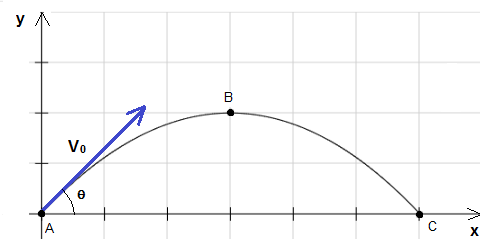
Ecuaciones de Proyectiles con Explicaciones

Considere un proyectil que se lanza con una velocidad inicial v₀ en una dirección que forma un ángulo θ con la horizontal. Suponemos que la resistencia del aire es despreciable y que la única fuerza que actúa sobre el objeto es la fuerza de gravedad con una aceleración g = 9.8 m/s². También se puede utilizar un applet html 5 interactivo para comprender mejor las ecuaciones del proyectil. Problemas de proyectiles con soluciones también se incluyen en este sitio.

Velocidad, Aceleración y Desplazamiento del Proyectil

La velocidad inicial V₀, siendo una cantidad vectorial, tiene dos componentes:
V_0x y V_0y dadas por
V_0x = V₀ cos(θ)
V_0y = V₀ sin(θ)
La aceleración A es también un vector con dos componentes A_x y A_y dadas por
A_x = 0 y A_y = - g = - 9.8 m/s²
A lo largo del eje x, la aceleración es igual a 0 y, por lo tanto, la velocidad V_x es constante y se da por
V_x = V₀ cos(θ)
A lo largo del eje y, la aceleración es uniforme y igual a - g y la velocidad en el tiempo t se da por
V_y = V₀ sin(θ) - g t
A lo largo del eje x, la velocidad V_x es constante y, por lo tanto, la componente x del desplazamiento se da por
x = V₀ cos(θ) t
A lo largo del eje y, el movimiento es de tipo aceleración uniforme y la componente y del desplazamiento se da por
y = V₀ sin(θ) t - (1/2) g t²

Forma de la Trayectoria del Proyectil

La forma de la trayectoria seguida por el proyectil se encuentra de la siguiente manera
Resuelve la fórmula \( \; x = V_0 cos(\theta) t \; \) para \( t \) para obtener \[ t = \dfrac{x}{V_0 cos(\theta)} \]
Sustituye \( t \) por \( \dfrac{x}{V_0 cos(\theta)} \) en la expresión anterior de y para obtener
\[ y = \dfrac{V_0 \sin(\theta) x}{V_0 \cos(\theta)} - (1/2) g \left( \dfrac{x}{V_0 \cos(\theta)} \right)^2 \]
Simplifica
\[ y = - \dfrac{g \; x^2}{2( V_0 \cos(\theta))^2} + x \tan(\theta) \]
La ecuación anterior es la trayectoria del proyectil, que es una parábola de la forma
\( y = A x^2 + B x \)
donde \( A = - \dfrac{g}{2( V_0 \cos(\theta))^2} \) y \( B = \tan(\theta) \)

Tiempo de Vuelo del Proyectil

El tiempo de vuelo es el tiempo que tarda el proyectil en ir desde el punto A hasta el punto C (ver figura anterior).
Se calcula estableciendo y = 0 (y = 0 en el punto C) y resolviendo para t
y = V₀ sin(θ) t - (1/2) g t² = 0
Factoriza t en la ecuación anterior
t(V₀ sin(θ) - (1/2) g t) = 0
Dos soluciones:
t = 0 (corresponde al punto A)
y
t = 2 V₀ sin(θ) / g (corresponde al punto C)
Por lo tanto, el tiempo de vuelo = 2 V₀ sin(θ) / g

Tiempo de Vuelo = 2 V₀ sin(θ) / g

Altura Máxima del Proyectil (correspondiente al punto B en la figura anterior)

En el punto B de la figura anterior, el proyectil está momentáneamente horizontal y, por lo tanto, la componente vertical de su velocidad es igual a cero. Por lo tanto
V_y = V₀ sin(θ) - g t = 0
Resuelve para t para obtener
t = V₀ sin(θ) / g (Nota: este es la mitad del tiempo de vuelo debido a la simetría de la parábola)
Sustituye t por V₀ sin(θ) / g en la expresión de y, obtenemos la altura máxima

\( H = \dfrac{V_0 \sin(\theta) V_0 \sin(\theta)}{g} - (1/2) \dfrac{}{} g \left( \dfrac{V_0 \sin(\theta)}{g} \right)^2 = \dfrac{(V_0 \sin(\theta))^2}{2 g} \)

Altura Máxima (en el punto B) = \(\dfrac{(V_0 \sin(\theta))^2}{2 g} \)

Rango Horizontal de un Proyectil (distancia AC en la figura anterior)

La distancia AC, que es el rango horizontal, es igual a x cuando t es igual al tiempo de vuelo 2 V₀ sin(θ) / g obtenido anteriormente. Por lo tanto
rango AC = x = V₀ cos(θ) t en t = tiempo de vuelo = 2 V₀ sin(θ) / g
Sustituye t por 2 V₀ sin(θ) / g y simplifica para obtener el rango AC
AC \( = V_0 cos(\theta) 2 V_0 sin(\theta) / g = V_0^2 sin(2\theta) / g \)