Since forces are represented by vectors, they can be added in the same way as vectors. There are two ways to add forces.
1 - Geometrical Addition of Forces
The example below shows the addition of 3 forces: F1, F2 and F3 on the left. On the right are the same forces shifted such that they are parallel to the given forces and arranged such that the final point of the first force (F1) coincides with the initial point of the second force (F2); the final point of the second force coincides with the initial point of the third force (F3). The sum R of the 3 forces has the start point of the first force in the addition and the final point of the last force in the addition.
2 - Analytical Addition of Forces Using Components
Forces given by their components are added by adding their x and y
components.
If for example F1 = ( F1x , F1y) and F2 = (F2x , F2y), then
F1 + F2 = (F1x + F2x , F1y + F2y)
Examples with Detailed Solutions
Example 1
F1 and F2 are forces given by their magnitudes and directions in the figure below. Find the magnitude and direction of the force R = F1 + F2. The direction is defined as the angle between the positive x-axis and R.
Solution
Let us examine two methods.
Method 1: Geometric / Trigonometric; using cosine and sine laws
Using the cosine law, we can write
|R|2 = |F1 + F2|2 = |F1|2 + |F2|2 - 2 |F1| |F2| cos (25 + 44)
Use |F1| = 20 and |F2| = 30, we obtain
|R| = |F1 + F2| = √(202 + 302 - 2 (20)(30) cos (25 + 44)) ≈ 29.5 N
Use the sine law to find angle α
sin(α) / 30 = sin (25 + 44) / 29.5
Solve to find α ≈ 71.7°
the direction of F1 + F2 defined as the angle between F1 + F2 and the positive x axis is given by
α + 25 ≈ 96.7°
Method 2: Analytical using components
Express F1 and F2 using components
F1 = (20 cos 25° , 20 sin 25°) and F2 = (-30 cos 44° , 30 sin 44°)
F1 + F2 = (20 cos 25° , 20 sin 25°) + (-30 cos 44° , 30 sin 44°) = (20 cos 25° - 30 cos 44° , 20 sin 25° + 30 sin 44°) ≈ (-3.5 , 29.3)
|F1 + F2| = √ ( (-3.5)2 + 29.32) ≈ 29.5 N
Direction: If the initial point of F1 + F2 is at the origin, the terminal point of F1 + F2 is in quadrant II, hence the angle between the positive x-axis and F1 + F2 is given by
180° - |arctan (29.3 / - 3.5)| ≈ 96.8 °
The second method is more efficient (takes less time) than the first method when the number of forces to be added is more than 3.
A video with more examples at Resultant of Two Forces
Example 2
What is the magnitude and the direction of F3 in the system of three forces below so that F1 + F2 + F3 = 0?
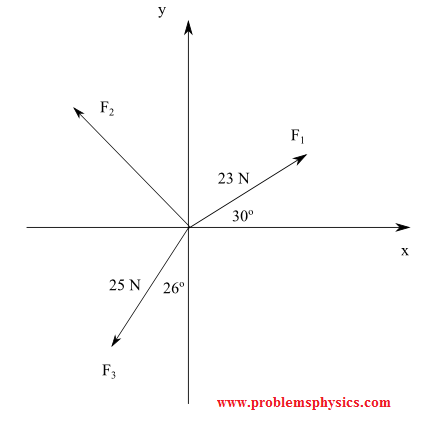
Solution
Express F1, F2 and F3 by their components
F1 = (23 cos 30° , 23 sin 30°)
F2 = (|F2| cos θ , |F2| sin θ) , where θ is the angle between the positive x-axis and F2
F1 = (-25 sin 26° , - 25 cos 26°)
(23 cos 30° , 23 sin 30°) + (|F2| cos θ , |F2| sin θ) + (- 25 sin 26° , - 25 cos 26°) = 0
23 cos 30° + |F2| cos θ - 25 sin 26° = 0
23 sin 30° + |F2| sin θ - 25 cos 26° = 0
The above equations give
|F2| cos θ = 25 sin 26° - 23 cos 30° ≈ -9.0
|F2| sin θ = 25 cos 26° - 23 sin 30° ≈ 10.1
|F2|2 = (25 sin 26° - 23 cos 30°)2 + (25 cos 26° - 23 sin 30°)2
|F2|2 ≈ 13.9 N
θ = 180 - arctan(10.1 / 9.0) ≈ 131.7°
Example 3
What is the relationship between the magnitudes |W| and |N| of forces W and N, with W directed in the negative y-axis direction and N in the positive y-axis direction and such that W + N = 0?
Solution
We first express W and N by their components as follows
W = (0 , -|W|) and N = (0 , |N|)
W + N = (0 , -|W|) + (0 , |N|) = 000000
Using the y-components, we obtain
-|W| + |N| = 0
|W| = |N|
More References and links