Being a vector, a force can be represented by its components like any vector. One of the main advantages of resolving forces into their components is that it simplifies operations like vector addition and scalar multiplication.
If \(|\vec{F}|\) is the magnitude and \(\theta\) is the angle between the positive direction of the x-axis and the force \(\vec{F}\), then the components \(F_x\) and \(F_y\) are given by:
\[F_x = |\vec{F}| \cos\theta \quad \text{and} \quad F_y = |\vec{F}| \sin\theta\]
Hence, \(\vec{F}\) may be written in terms of its components as follows:
\[\vec{F} = (F_x, F_y) = (|\vec{F}| \cos\theta, |\vec{F}| \sin\theta) \quad (I)\]
A video with more examples on Components of Vectors and another video with more examples on Components of Forces are included.
Find the components of a force \(\vec{F}\) whose magnitude is 20 N and its direction is defined by angle \(\theta = 30^\circ\) made by the force and the positive x-axis as shown below.
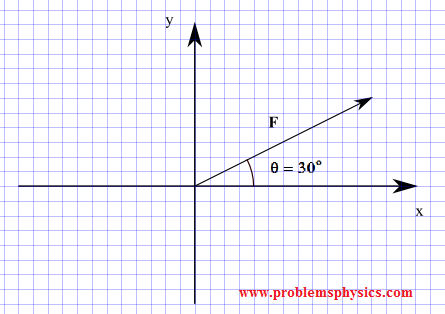
Solution
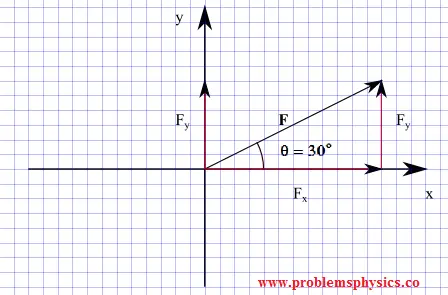
Use formula (I) above to find the components of \(\vec{F}\)
The angle from the positive x-axis to \(\vec{F}\), in anticlockwise direction is \[ \theta = 30^\circ \], hence
\[F_x = |\vec{F}| \cos \theta = 20 \cos 30^\circ = 10\sqrt{3}\]
\[F_y = |\vec{F}| \sin \theta = 20 \sin 30^\circ = 10\]
\[\vec{F} = (10\sqrt{3}, 10)\]
Find the components of a force whose magnitude is 50 N and its direction is given by angle \(\alpha = 25^\circ\) made with the negative y-axis in the direction of negative x axis as shown in the diagram below.
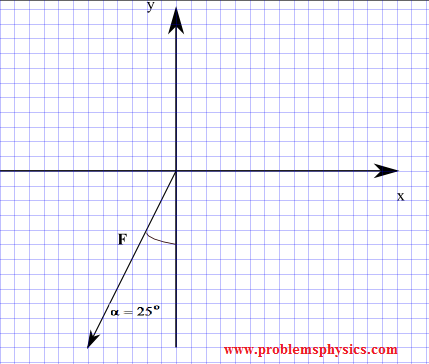
Solution

The angle from the positive x-axis to the force \(\vec{F}\) is \[ \theta = (270 - \alpha)^\circ \]
Using formula (I), \(F_x\) and \(F_y\) be the components of \(\vec{F}\) as shown in the diagram above.
\[ F_x = |\vec{F}| \cos \theta = 50 \cos (270-25)^\circ = - 50 \sin(25^\circ) = \approx -21.1 \]
\[ F_y = |\vec{F}| \sin \theta = 50 \sin (270-25)^\circ = - 50 \cos(25^\circ) \approx -45.3 \]
\[\vec{F} = (-21.1, -45.3)\]
In the diagram below, force \(\vec{F}\) is parallel to the leg CB of the right triangle ABC.
a) Determine the components of the force \(\vec{F}\) in terms of the magnitude of \(\vec{F}\) and angle \(\alpha\). The rectangular system x-y has the x-axis parallel to AC and the y axis perpendicular to AC as shown in the diagram.
b) Find numerical values of the components for \(|\vec{F}| = 100 \text{ N}\) and \(\alpha = 30^\circ\).
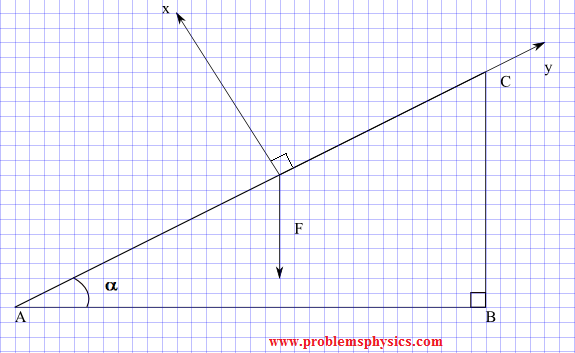
Solution
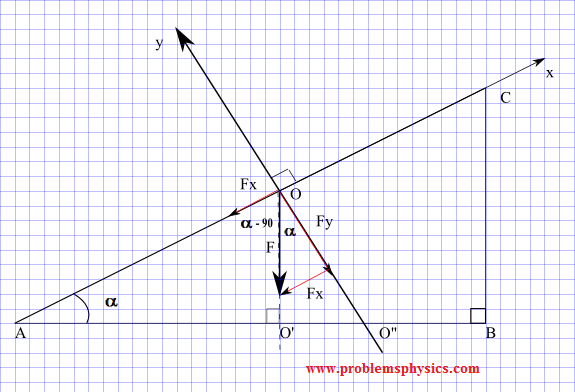 a)
a) Examine the system of axes and see the angle from the positive x axis to \(\vec{F}\) is : \[ \theta = 270^{\circ} - \alpha \] Use formula (I) to write :
\[F_x = |\vec{F}| \cos \theta = \cos(270^{\circ} - \alpha) \] \[F_y = |\vec{F}| \sin \theta = \sin (270^{\circ} - \alpha) \] Use knwowing that \( \cos 270^{\circ} = 0 \) and \( \sin 270^{\circ} = -1 \), use the trigonometic formulas to write: \[ \cos(270^{\circ} - \alpha) = \cos 270^{\circ} \cos \alpha + \sin 270^{\circ} \sin \alpha = - \sin \alpha \] \[ \sin(270^{\circ} - \alpha) = \sin 270^{\circ} \cos \alpha - \cos 270^{\circ} \sin \alpha = - \cos \alpha \] Hence \[\vec{F} = (-|\vec{F}| \sin \alpha, -|\vec{F}| \cos \alpha)\]
The right triangle AOO' has angle \(\alpha\), \(90^\circ-\alpha\) and \(90^\circ\).
Since AC is perpendicular to OO", angle AOO' is equal to \(90^\circ\) and therefore angle O'OO" is equal to \(\alpha\).
Consider the right triangle made by \(\vec{F}\), \(F_y\) and \(F_x\).
\[\sin \alpha = -\frac{F_x}{|\vec{F}|} \quad \text{(the minus sign is due to the fact that \(F_x\) is negative)}\] \[\cos \alpha = -\frac{F_y}{|\vec{F}|} \quad \text{(the minus sign is due to the fact that \(F_y\) is negative)}\]
which gives:
\[F_x = -|\vec{F}| \sin \alpha\] \[F_y = -|\vec{F}| \cos \alpha\] \[\vec{F} = (-|\vec{F}| \sin \alpha, -|\vec{F}| \cos \alpha)\]
b)For \(|\vec{F}| = 100 \text{ N}\) and \(\alpha = 30^\circ\):
\[F_x = -|\vec{F}| \sin \alpha = -100 \sin 30^\circ = -50\] \[F_y = -|\vec{F}| \cos \alpha = -100 \cos 30^\circ = -50\sqrt{3}\] \[\vec{F} = (-50, -50\sqrt{3})\]
Note: The above example is very useful in problems related to forces in inclined plane.
Three forces \(\vec{F}_1\), \(\vec{F}_2\) and \(\vec{F}_3\) of magnitudes 80 N, 60 N and 50 N in the same system of axes such that \(\vec{F}_1\) is directed along the positive x axis; \(\vec{F}_2\) in the direction given by the bearing N25E and \(\vec{F}_3\) along the negative y axis.
Find the components of each force.
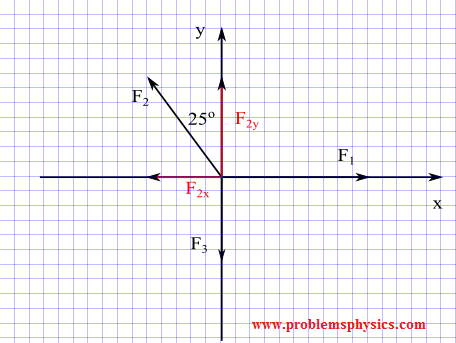
Solution
We first construct a diagram using the directions given above.
\(\vec{F}_1\) is directed along the x axis, hence one component along the x axis equal to \(|\vec{F}_1|\) and the component along y-axis is equal to 0:
\[\vec{F}_1 = (|\vec{F}_1|, 0) = (80, 0)\]
\(\vec{F}_3\) is directed along the negative y axis, hence:
\[\vec{F}_3 = (0, -|\vec{F}_3|) = (0, -50)\]
\(\vec{F}_2\) is such that the x component is positive and the y component is positive; using the right triangle made by \(\vec{F}_2\), \(F_{2x}\) and \(F_{2y}\) we write:
\[\vec{F}_2 = (F_{2x}, F_{2y}) = (60 \cos(90+25)^\circ, 60 \sin (90+25)^\circ) = -60 \sin(25^\circ) , 60 \cos(25^\circ)\]
Express each of the forces A, B, C and D shown in the figure below by its components.
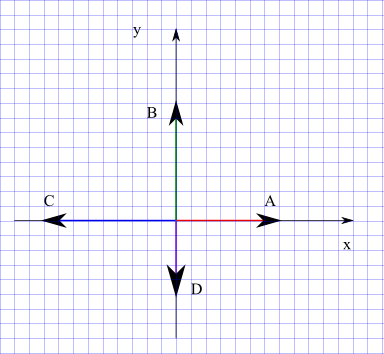
Solution
Each of the four forces is directed either along the x or the y axis in the negative or positive direction.
| Force | X-Component | Y-Component | Vector Form |
|---|---|---|---|
| A | \(|\vec{A}| \cos 0^\circ = |\vec{A}|\) | \(|\vec{A}| \sin 0^\circ = 0\) | \(\vec{A} = (|\vec{A}|, 0)\) |
| B | \(|\vec{B}| \cos 90^\circ = 0\) | \(|\vec{B}| \sin 90^\circ = |\vec{B}|\) | \(\vec{B} = (0, |\vec{B}|)\) |
| C | \(|\vec{C}| \cos 180^\circ = -|\vec{C}|\) | \(|\vec{C}| \sin 180^\circ = 0\) | \(\vec{C} = (-|\vec{C}|, 0)\) |
| D | \(|\vec{D}| \cos 270^\circ = 0\) | \(|\vec{D}| \sin 270^\circ = -|\vec{D}|\) | \(\vec{D} = (0, -|\vec{D}|)\) |
| Principle | Mathematical Expression | Description |
|---|---|---|
| Component Formulas | \(F_x = |\vec{F}| \cos\theta\), \(F_y = |\vec{F}| \sin\theta\) | Basic trigonometric relations for finding components |
| Magnitude from Components | \(|\vec{F}| = \sqrt{F_x^2 + F_y^2}\) | Pythagorean theorem applied to force components |
| Direction Angle | \(\theta = \tan^{-1}\left(\frac{F_y}{F_x}\right)\) | Angle calculated from components (consider quadrant) |
| Vector Addition | \(\vec{R} = \vec{A} + \vec{B} = (A_x + B_x, A_y + B_y)\) | Resultant force from component-wise addition |
| Quadrant | X-Component Sign | Y-Component Sign | Angle Range |
|---|---|---|---|
| I | Positive (+) | Positive (+) | \(0^\circ \text{ to } 90^\circ\) |
| II | Negative (-) | Positive (+) | \(90^\circ \text{ to } 180^\circ\) |
| III | Negative (-) | Negative (-) | \(180^\circ \text{ to } 270^\circ\) |
| IV | Positive (+) | Negative (-) | \(270^\circ \text{ to } 360^\circ\) |