DC Voltage Divider Calculator
An online calculator to calculate the output voltage, current and power of a load in dc voltage divider is presented. Activities using the calculator to investigate the maximum power delivered to the load \( R_L \) are suggestsed.
Current, Voltage and Power Formulas
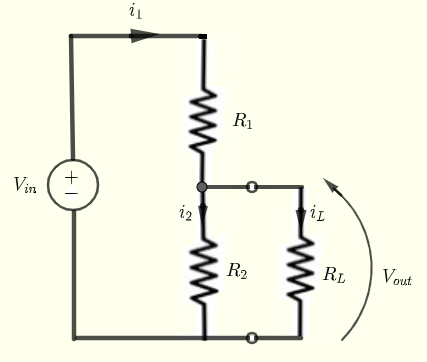
Given \( V_{in} \) , \( R_1 \) , \( R_2 \) and the load \( R_L \), let us find formulas for the current \( i_L \) through, the voltage \( V_L \) across, and the power delivered to the load (resistor) \( R_L \).
Using Kirchhoff's laws of voltage and current, we can write the following equations:
\( V_{in} = R_1 i_1 + R_2 i_2 \) (I)
\( - R_2 i_2 + R_L i_L = 0 \) (II)
\( i_1 = i_2 + i_L \) (III)
Substitute \( i_1 \) in equation (I) by \( i_2 + i_L \) to obtain two equations with two unknowns \( i_2 \) and \( i_L \)
\( V_{in} = R_1 (i_2 + i_L) + R_2 i_2 \) (I')
\( - R_2 i_2 + R_L i_L = 0 \) (II')
Solve the above system of two equations and two unknowns by any method to obtain
\( i_L = \dfrac{R_2}{R_L(R_1+R_2)+R_1 R_2} V_{in} \)
Use Ohm's to find \( V_L \):
\( V_L = R_L i_L = \dfrac{R_2 R_L}{R_L(R_1+R_2)+R_1 R_2} V_{in} \)
The power \( P_L \) delivered to the load is given by
\( P_L = V_L i_L \)
dc Voltage Divider Calculator
Enter the resistances of \( R_1 \) , \( R_2 \), \( R_L \) in Ohms and the source voltage \( V_{in} \) in volts as positive real numbers and press "Calculate". The outputs are the current \( i_L \) through \( R_L \), the voltage \( V_L \) across \( R_L \) and the power \( P_L \) delivered to the load \( R_L \).
Outputs
Activities
It can be shown that when \( R_L = \dfrac{R_1 R_2}{R_1 + R_2} \), the power delivered to the load \( R_L \) is maximum.
Select values for \( R_1 \) and \( R_2 \) and calculate \( R_L \) using the formula \( R_L = \dfrac{R_1 R_2}{R_1 + R_2} \) and use all three values in the calculator above to calculate \( P_L \).
Then keep \( R_1 \) and \( R_2 \) with the same values selected above but change \( R_L \) slightly above or below the calculated value. Which value of \( R_L \) gives the maximum value of \( P_L \).
Example
Let \( R_1 = 20 \) and \( R_2 = 30 \), hence \( R_L = \dfrac{20 \times 30}{20 + 30} = 12 \)
Enter the values \( R_1 = 20 \), \( R_2 = 30 \) and \( R_L = 12 \) in the Calculator.
What is the values of \( P_L \)?
Keep \( R_1 = 20 \) and\( R_2 = 30 \) but change \( R_L \) to values different from 12, higher values such as 13, 14, 15, ... and lower values such as 11, 10, 9 ...and take note of the values of \( P_L \).
Which value of \( R_L \) gives the highest value of \( P_L \)?
More References and Links
Ohm's law with Examples
Kirchhoff's Law of Circuits with Examples
Electricity
Free SAT II Physics Practice Solutions on
DC Electric Circuits

